Implementation description

Note

This implementation for the moment only deals with encoding and formatting the payload for the image data. It does not support the formatting of the variables necessary for decoding (frequency values of the DCT and size of the image). What can be recommended for the moment is to use a common general frequency table for the DCT values.

The jpgedna package has been implemented in the most modular way possible. We aim at making a code that people will be able to experiment with.

Coders

Principle

The main purpose of the jpegdna algorithm is to encode the DCT coefficients into quaternary code instead of binary. To achieve this, we use a series of coders that are the core of our implementation. Since these coders play such an important role, we have decided to orient the development around them. We defined a standard that all of our coders follow:

• Inherit from the abstract class coders.AbstractCoder

• Implement the abstract methods mycoder.encode(inp) and mycoder.decode(code)

• Both those methods only communicate with the user, the data to be encoded or decoded and the data result

• Additionnal arguments can be set or accessed by implementing the mycoder.set_state(*args) and mycoder.get_state() metods

• Those arguments will be defined as attributes, mycoder.set_state(*args) and mycoder.get_state() are a setter and a getter

• The mycoder.full_encode() or mycoder.full_decode() methods can be overloaded to describe the full encoding or decoding process (initialisation, encoding, return of arguments)

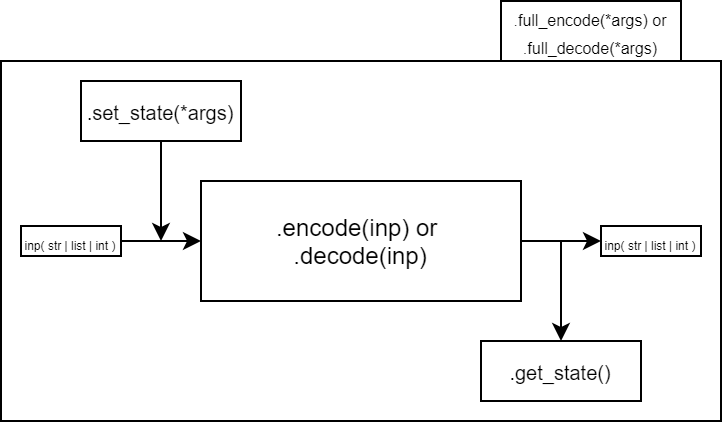
To implement a new coder, following these requirements will suffice and render the use of the coder easy. The encode and decode methods quickly help to define the payload of the data that you encode, and the getters and setters help with identifying what might be needed in some headers for the well funcitonning of the whole coder.

The coders that have already been implemented are the following:

Goldman Coder

The Goldman Coder is instantiated with the alphabet that will be in use for the coder: coder = jpegdna.coders.GoldmanCoder(alphabet).

The coder uses strings as input and output and does not need any initialization. A wrapper coder = jpegdna.coders.GoldmanCoder(alphabet) has been made for the specific case where we use DNA.

class jpegdna.coders.goldmancoder.GoldmanCoder(alphabet, verbose=False)

Goldman coder

Parameters

alphabet (list) – alphabet for encoding

Return type

None

decode(code)

Function that decodes DNA data using Goldman coder

Parameters

code (str) – Signal to be decoded

Returns

Decoded signal

Return type

str

encode(inp)

Function that encodes data into DNA using Goldman coder

Parameters

inp (str) – Signal to be encoded

Returns

Encoded signal

Return type

str

Huffman Coder

The Huffman n-ary coder is instanciated with 3 parameters: the alphabet on which it is defined, the frequencies of appearance for the alphabet members, and the integer describing the arity of the tree. coder = jpegdna.coders.HuffmanCoder(alphabet, freqs, arity)

The encoder takes a list of alphabet members as input, and outputs a string of integers between 0 and n-1, n being the arity of the tree. The decoder inverses the types for input and output.

class jpegdna.coders.huffmancoder.HuffmanCoder(*args, verbose=False)

Huffman n-ary tree coder

case 1:

Parameters

• alphabet (list) – List of elements that can be encoded

• feqs – List of appearence frequencies for each element in the alphabet

• n (int) – base of the n-ary tree

• verbose – bool

• debug – bool

Variables

• verbose – Verbosity enabler

• debug – Verbosity for debug enabler

case 2:

Parameters

dic (dict) – Huffman dictionnary

decode(code)

Decode a signal using the Huffman n-ary dictionnary

Parameters

code (str) – Signal to be decoded

Returns

Decoded signal

Return type

list

encode(inp)

Encode a signal using a Huffman n-ary dictionnary

Parameters

inp (list) – Signal to be encoded

Returns

Encoded signal

Return type

str

find_codeword_key(word)

Find the symbol associated with a codeword in the huffman dictionnary

Parameters

word (str) – codeword for which we want the symbol

Returns

Symbol in the alphabet corresonding to the codeword

Return type

str

Coefficient coder

The coefficient coder is the part that takes care of encoding the coefficient sequence obtained after quantizing the DCT coefficients. There are two different ones, one that is used for DC coefficients and one for AC coefficients only.

The DC coefficient is first diferrentially coded, meaning instead of encoding the coefficient, we encode the difference between itself and the DC coefficient of the previous block. Then the difference result is encoded using a combination of the category coder and the value coder. The category of a coefficient is an integer that is related to the absolute value of the coefficient. In the case where we use the paircode algorithm developed by Melpomeni Dimopoulou, in function of the relation table between the values and their category is:

Category Value relation table example

Category	Negative coefficients	Positive coefficients
1	[-5, -1]	[1, 5]
2	[-25, -6]	[6, 25]
3	[-75, -26]	[26, 75]
4	[-275, -76]	[76, 275]
5	[-775, -276]	[276, 775]
6	[-2775, -776]	[776, 2775]
7	[-7775, -2776]	[2776, 7775]
8	[-27775, -7776]	[7776, 27775]

The category coder will basically encode this category into a DNA word using a dictionnary of codewords for each possible category. Introducing a concept of category for the coefficients is very helpful beacause it can help with allocating an appropriate number of nucleotides necessary to encode the real value of the coefficient. This is the role of the value coder.

An important part of the coefficient decoder is the get_state() method because it gives back a value called num_bits that essentially describes the number of bits used to encode the current coefficient. That way, when you decode the coefficient, you can resynchronize your position in the quaternary stream once it is done.

Category Coder

The category coder simply encodes the possible values of the category using a dictionnary. This dictionnary is generated using the Huffman algorithm with a ternary tree. As described earlier, this will give us a dictionnary of codewords composed of digits between 0 and 2. Those codewords are then encoded into DNA using a goldman encoder with the rotating [A, T, C, G] alphabet. A rotating alphabet is an alphabet where you take out the element that you previously used, to avoid repetitions. You put the element back in the alphabet after having written a different element, meaning one step after taking it back. The order of the rotating alphabet is always the same: we don’t append the element at the end of the alphabet but at the place it was before. Having a ternary tree for the Huffman encoder was obviously a choice to be able to encode the words into a 4-element alphabet with the goldman encoder.

Value Coder

The value coder is the coder that is in charge of encoding the coefficient value according to the category in which it lies. It is based on the use of a codebook of codewords of fixed length. The bigger the category , the longer the codewords and the bigger the codebook. For encoding, you use the codeword that has as index the coefficient value. For decoding, you search the index of the codeword in the codebook. The codebook only changes in function of the category.

Transforms

Principle

The same kind of modularity principle has been applied when developping transforms.

• Inherit from the abstract class transforms.AbstractTransform

• Implement the abstract methods mytransform.forward(inp) and mytransform.inverse(code)

• Both those methods only communicate with the user, the data to be encoded or decoded and the data result

• Additionnal arguments can be set or accessed by implementing the mytransform.set_state(*args) and mytransform.get_state() metods

• Those arguments will be defined as attributes, mytransform.set_state(*args) and mytransform.get_state() are a setter and a getter

• The mytransform.full_forward() or mytransform.full_inverse() methods can be overloaded to describe the full encoding or decoding process (initialisation, encoding, return of arguments)

The transforms that have already been implemented are the following:

Color Conversion Transform

The color conversion that we use is just a wrapper of the cv2.cvtColor function.

class jpegdna.transforms.colortransform.RGBYCbCr

RGB YCbCr color converter

forward(inp)

Wrapper method to covert RGB to YCbCr

Parameters

inp (np.array) – Input image

Returns

YCbCr image

Return type

np.array

inverse(inp)

Wrapper method to covert YCbCr to RGB

Parameters

inp (np.array) – Input YCbCr image

Returns

RGB image

Return type

np.array

Discrete Cosine Transform

The Discrete Cosine Transform that we use is just a wrapper of the scipy.fftpack.dctn and scipy.fftpack.idctn functions. It converts from RGB with .forward() to YCbCr an back with .inverse().

class jpegdna.transforms.dctransform.DCT

For Jpeg

forward(inp)

Forward 2D DCT

Parameters

inp (np.array) – input image block

Returns

DCT coefficients

Return type

np.array

full_forward(inp, *args)

Forward 2D DCT

Parameters

• inp (np.array) – input image block

• norm (str) – Type of DCT (default: None)

Returns

DCT coefficients

Return type

np.array

full_inverse(inp, *args)

Inverse 2D DCT

Parameters

• inp (np.array) – input image block

• norm (str) – Type of DCT (default: None)

Returns

DCT coefficients

Return type

np.array

inverse(inp)

Inverse 2D DCT

Parameters

inp (np.array) – DCT coefficients

Returns

image block

Return type

np.array

Channel Sampler Transform

This transform contains different samplers for color channels. You sample using .forward(), it returns a tuple containgin the 3 channels with different sizes. Desampling is done using .inverse(), it gives back a 3 channel image. To get the appropriate sampler, you instantiate the class with the name of the sample, for example ChannelSampler(sampler=”4:2:2”). Available samplers are: "4:2:2", "4:2:0", "4:1:1", "4:4:4", "4:4:0".

class jpegdna.transforms.sampler.ChannelSampler(sampler='4:2:2')

Channel Sampler

Variables

sampler – Sampler name (default: “4:2:2”)

Parameters

sampler – str

forward(inp)

Sampling method

Parameters

inp (np.array) – 3-channel image

Returns

Tuple of the 3 sampled channels (Y not subsampled usually)

Return type

tuple

get_sampler()

Get sampler name

inverse(inp)

Desampling method

Parameters

inp (np.array) – Tuple of the 3 sampled channels (Y not subsampled usually)

Returns

3-channel image

Return type

np.array

set_sampler(sampler)

Set sampler from its name

Zig-Zag Transform

This transform is used to organize the DCT quantized values that are in a block in a 1-dimentional sequence of values and backwards. The forward takes a 2D array as input and outputs a 1D array and the inverse has inverse inputs and outputs.

For the inverse transform, it is required to set the expected block dimensions for the output using zigzag.ZigZag.set_state(width, height).

class jpegdna.transforms.zigzag.ZigZag(verbose=False)

Zig-zag transform

Variables

• verbose – Verbosity enabler

• vmax (int) – width of the matrix

• hmax (int) – height of the matrix

Parameters

verbose – bool

forward(inp)

Transform the inp matrix into a sequence element following the zig-zag reading order

Parameters

inp (np.array) – Input to be transformed

Returns

Zig-zag read sequence

Return type

np.array

full_inverse(inp, *args)

Inverse transform wrapper method

Parameters

• inp – Input to apply inverse transform

• args (any) – Supplementary arguments for the inverse transforms

Type

any

Returns

Inverse transformed message

Return type

any

inverse(inp)

Reconstruct matrix from a sequence of zig-zag read values

Parameters

inp (np.array) – Sequence of values

Returns

reconstructed matrix

Return type

np.array

set_state(*args, case=None)

Sets the state of the transform

Parameters

• hmax –

• vmax (int) –

Formatting

Principle

The formatting into oligos (small strands of size ~200 to reduce noise) of the compression result and the deformatting of those oligos to decompress an image is a totaly different layer in the general compression workflow. What this formatting needs to do is to gather all the data necessary to decode the image, meaning: the strand representing the content data, information on the frequencies that are used(from the image or from precalculated frequencies), the frequencies that should be transmitted if frequencies were computed from the image, the dimensions of the image, in the case of RGB, the sampler that was used.

Three formats of oligos will be used to format the data:

The first format is the one that will be used for the strand coming out of the compression, meaning the imag data in itself: These oligos will contain: an identifier making it possible during formatting to recognise that these are oligos related to the image data, and offset index, and a small slice of the image data strand. The offset indices indicate the order of appearance of the slices in the full data strand: during deformatting, the general data strand is reconstructing by reordering the slices according to this index.

This format is defined in the class named GeneralInfoFormatter in the format module.

class jpegdna.format.generalinfoformatter.GeneralInfoFormatter(alpha, freq_origin, m, n, blockdims, max_cat, max_runcat, dc_freq_len, ac_freq_len, image_type, sampler, header, oligo_length=200, debug=False)

Formatter for the general information related to the compression

Variables

• alpha – alpha value of the compression, if it is known

• freq_origin – origin of the frequencies (“default” or “from_img”)

• m – first dimension of the image

• n – second dimension of the image

• blockdims – dimensions of the block used for DCT

• max_cat – max value for the categories

• max_runcat – max value for the run/categories

• dc_freq_len – codeword length for encoding the dc frequencies

• ac_freq_len – codeword length for encoding the ac frequencies

• oligo_length – Size of the oligos used for formatting

colored_image()

Check if image is colored or gray level

Return type

bool

deformat(oligos)

Decoding method

Parameters

code (list) – Formated oligos to deformat

Returns

Deformated strand

Return type

str

format(inp)

Encoding method

Parameters

inp (str) – Strand to format

Returns

Formatted oligos

Return type

list

The second format available will concern the frequencies. Since those frequencies are number tables, they are first encoded into a two DNA strands using a codebook of fixed-length DNA codewords. One strand will concern DC categories, and one will concern AC run/categories. The values of the DC and AC categories or run/categories frequencies will be decoded from the two strands using the same codebook. The oligos for those frequencies will finally be similar to the data ones. It will contain an identifier specifying that it is a frequency oligo, an identifier stating if it is a DC or AC frequency oligo, an offset index and a samll slice of the AC or DC frequency strand.

This format is defined in the classes named GrayFrequenciesFormatter and RGBFrequenciesFormatter in the format module.

class jpegdna.format.frequenciesformatter.GrayFrequenciesFormatter(max_cat, max_runcat, dc_freq_len, ac_freq_len, header, dc_header, ac_header, oligo_length=200, debug=False)

Formatter for the gray DC and AC frequencies

Variables

• max_cat – max value for the categories

• max_runcat – max value for the run/categories

• dc_freq_len – codeword length for encoding the dc frequencies

• ac_freq_len – codeword length for encoding the ac frequencies

• oligo_length – Size of the oligos used for formatting

decode_frequencies(strand, freq_type)

Decode the frequencies using fixed-length codebooks

Parameters

• strand (str) – encoded frequency values

• freq_type (str) – DC/AC frequency indicator

Returns

list of frequency values

Return type

list(int)

deformat(oligos)

Deformats and decodes both DC and AC frequency oligos

Parameters

oligos (list(str)) – formatted frequency oligos for AC and DC

Returns

decoded frequency tables

Return type

tuple(list(int))

deformat_frequencies(oligos)

Deformat the oligos describing either the DC or the AC frequencies

Parameters

• oligos – oligos to deformat

• freq_type (str) – DC/AC frequency indicator

Returns

strand encoding the frequencies

Return type

str

encode_frequencies(freqs, freq_type)

Encode the frequencies using fixed-length codebooks

Parameters

• freqs (list(int)) – frequency values to encode

• freq_type (str) – DC/AC frequency indicator

Returns

strand encoding the frequencies

Return type

str

format(inp)

Encodes and formats both DC and AC frequencies

Parameters

inp (tuple(list(int))) – frequencies for DC categories and AC run/categories

Returns

formatted frequency oligos

Return type

list(str)

format_frequencies(inp, freq_type)

Format the strand encoding either the DC or the AC frequencies

Parameters

• inp (str) – strand to format

• freq_type (str) – DC/AC frequency indicator

Returns

formatted AC or DC frequency oligos

Return type

list(str)

Finally, a third type of oligo will concern one single oligo that will encode all the necessary data for deformatting and for decoding: It contains: the size of the image, the size of the blocks for the DCT, the value of the dynamic used, the length of the codewords used to encoded the frequencies in the frequency oligos. Since these informations are crucial to ensure deformattability/decodability of the data, they are encoded using barcodes, meaning that the codebooks used to encode the alpha values, … contain codewords that have an bigger edit distance. That way, if because of the noise modifies the codeword, we can try to get it back by finding the closest codeword present in the codebook.

This format is defined in the class named DataFormatter in the format module.

class jpegdna.format.dataformatter.DataFormatter(header, oligo_length=200, debug=False)

Formatter for the strand coming out of the compression algorithm

Variables

oligo_length – Size of the oligos used for formatting

deformat(oligos)

Methods deformatting the oligos and rebuilding the data strand

Parameters

oligos (list(str)) – data oligos

Returns

data strand resulting from compression

Return type

str

format(inp)

Method formatting the data strand into oligos

Parameters

inp (str) – strand resulting from the compression algorithm

Returns

list of formatted oligos of size self.oligo_length

Return type

list(str)

In addition to the formatting that was described earlier, all the oligos will contain a sense nucleotide at each end indicating in which sense it should be read, an parity check that will act like a checksum, containing four oligos, each of them checking the parity of one base (A, T, C, G). They will also contain an identifier that is unique for every image in the oligo pool. Finnaly for real usecase applications, one can need to add primers for sequencing machines. We already included in the code the case where people want to use illumina primers.

All this formattingalgorithm has been integrated in the codecs. A boolean parameter called formatting is used at initialization of the codec to specify if one wants to use formatting or not.