Les listes: des données structurées¶
Au premier cours nous avons beaucoup travaillé sur des données atomiques comme les entiers, les flottants, les booléens, ou encore les caractères. Nous avons aussi vu quelques données structurées comme les tuples et les chaînes de caractères.
Ce cours-ci, nous allons nous focaliser sur les listes. Une liste est une suite finie de valeurs, et ces valeurs sont toutes du même type.
Les listes par énumération¶
On peut créer une liste par énumération, en séparant chacune de ses valeurs par un ; à l'intérieur de deux crochets.
let liste_entiers = [0;1;2;3;4;5;6;7;8;9]
let liste_booleens = [true] (* une liste à un seul élément! *)
Si toutes les valeurs de la liste sont du type t, le type de la liste est t list.
OCaml détermine tout seul le type de la liste.
Il nous empêche aussi de créer des listes mal typées; une liste est mal typée si elle contient au moins deux valeurs de types différents.
let liste_mal_typee = [0; 1; true]
OCaml détermine le type de la liste en regardant la première valeur qui apparait dans l'énumération.
Et pour la liste vide?
let liste_vide = []
Le type de la liste vide fait intervenir une variable de type, que nous avions déjà vues la semaine dernière dans le type de certaines fonctions.
On dit que c'est une liste polymorphe: OCaml pourra la voir comme une liste d'entiers ou comme une liste de booléens, selon les besoins de l'inférence de type.
Le module List¶
La longueur d'une liste est donnée par la fonction List.length
List.length liste_entiers
On avait déjà rencontré String.length la semaine dernière, pour calculer la longueur d'une chaîne de caractères. Ce deux fonctions portent deux noms différents, et en effet, ce sont bien deux fonctions différentes.
D'ailleurs toutes les fonctions sur les listes sont rangées dans un module qui s'appelle List.
List.rev [1;2;3] (* l'image mirroir de la liste *)
List.append [1;2;3] [4;5;6] (* la concaténation de deux listes *)
List.hd [1;2;3] (* l'élément de tête (head) de la liste *)
et ainsi de suite...
Notez bien que les listes ne sont pas mutables.
Toutes les fonctions sur les listes renvoient une nouvelle liste.
Elles ne peuvent pas modifier leur argument.
let l = [1;2;3]
let l2 = List.rev l
l
À propos de la notation List.¶
Au début on peut trouver cela pénible de devoir écrire List. à chaque fois.
En fait je pourrais demander à OCaml de rendre implicite le List.. Pourtant, dans ce cours, je ne le ferai pas! ceci pour éviter, entre autre, les confusions entre les fonctions length de modules différents, comme String.length.
En TP, vous pourrez toujours créer votre propre alias, par exemple let len = List.length et l'utiliser ensuite...
Et puis il y a d'autres solutions, qui permettent d'écrire length au lieu de List.length juste là où il faut, patience, on aura un cours tout entier sur les modules!
Notez par ailleurs que vous n'aurez pas à écrire List.append, OCaml offre une notation
alternative pour cette fonction
[1;2;3] @ [4;5;6] (* souvenez vous : @ = a, comme dans *a*ppend *)
La liste du débutant¶
let ma_liste = ['h','e','l','l','o'] in List.length ma_liste
OCaml dit que la liste ci-dessus est de longueur 1, et il a parfaitement raison.
Voyez-vous pourquoi?
Le type de ma_liste nous renseigne sur l'erreur que nous avons commise
let ma_liste = ['h','e','l','l','o']
Et oui, c'est une liste de quintuplets de caractères; elle contient un seul élément, qui est un quintuplet!
Pour obtenir une liste de cinq caractères, il aurait fallu écrire
let ma_liste = ['h';'e';'l';'l';'o']
List.length ma_liste
Méfiez-vous! Vous n'êtes plus en Python...
Notion de liste chaînée¶
La différence entre les listes d'OCaml et celles de Python dépasse très largement les histoires de syntaxe.
Les listes de Python sont ce qu'on appelle des tableaux extensibles. Toutes les valeurs sont rangées côte à côte en mémoire.
Les listes d'OCaml, en revanche, sont des listes chaînées. Chaque valeur est dans une cellule mémoire qui contient aussi l'adresse de la cellule suivante. Ces cellules sont rangées n'importe où en mémoire.
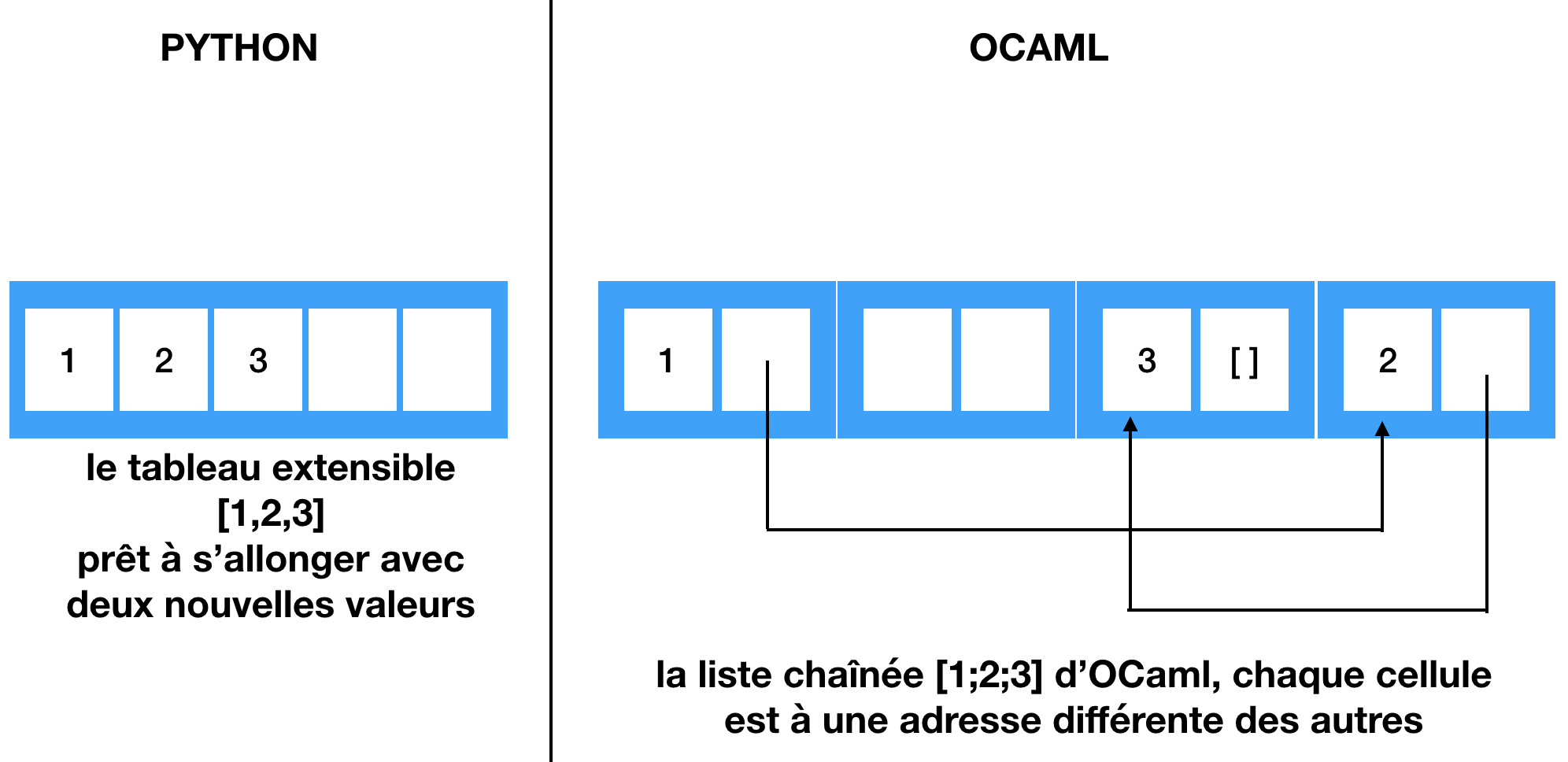
Les tableaux extensibles ont les mêmes soucis que les familles nombreuses: quand il n'y a plus de place, il faut déménager tout le monde, et plus il y a de monde, plus c'est couteux.
Les listes chaînées ont des soucis plus administratifs: quand on cherche le bureau 719, il faut d'abord frapper à la porte de 718 autres bureaux.
On peut dire que les listes chaînées sont plus "bas niveau" que les tableaux extensibles: elles peuvent s'avérer plus efficaces, encore faut-il les utiliser à bon escient. Et cela demande un peu d'expertise...
Ajouter une valeur en début de liste¶
Pour ajouter une valeur en début de liste, on utilise l'opérateur ::
let liste1 = [1; 2; 3]
let liste2 = 0 :: liste1
let liste3 = 9 :: 8 :: 7 :: liste1 (* = 9::(8::(7::liste1))) *)
Notez bien que liste3 ne contient pas le 0 qu'on a ajouté quand on a défini liste2: liste1 n'a pas été modifiée pendant la définition de liste2. N'oubliez pas, les listes ne sont pas mutables.
Ceci permet d'économiser de la mémoire et du temps de calcul en recopies. Par exemple, liste2 et liste3 peuvent partager sans risque liste1.
En comparaison, le partage avec une structure de données mutable est toujours risqué: si l'on changeait une valeur dans liste1, on changerait par la même occasion le contenu de liste2 et liste3, et ce n'est pas toujours ce qu'on veut faire...
Parcourir une liste chaînée¶
Pour parcourir une liste chaînée, il faut savoir suivre les flèches. Pour cela, on va avoir besoin de la fonction
List.tl, qui renvoie la queue (tail) de la liste.
let l = [1;2;3]
let l' = List.tl l
l (* n'a pas été modifié par List.tl... *)
List.tl []
Supposons par exemple que l'on n'ait pas la fonction List.length et que l'on veuille la reprogrammer.
On va pouvoir faire un calcul par récurrence, avec un cas de base et un principe de récurrence permettant de se ramener à une liste plus petite
let rec len li =
if li = [] (* si la liste vide *)
then 0 (* alors sa longueur vaut 0 *)
else 1 + len (List.tl li) (* sinon la longueur de sa queue + 1 *)
Définissons de même la fonction sum qui calcule la somme d'une liste d'entiers.
let rec sum li =
if li = []
then 0
else List.hd li + sum (List.tl li)
sum [1;2;3]
Les définitions par cas¶
Laissons les listes un instant, et supposons que nous voulions choisir au hasard l'une des chaînes de caractères "pierre", "feuille", ou "ciseaux" avec probabilité 1/3 chacune. On commence naturellement par tirer un nombre au hasard entre 0 et 2
let n = Random.int 3
Il reste ensuite à examiner la valeur de n pour renvoyer la chaîne de caractères qu'il code.
On peut utiliser une définition par cas de la forme match ... with ....
let tirage = match n with
| 0 -> "pierre"
| 1 -> "feuille"
| 2 -> "ciseaux"
| _ -> "erreur"
Chaque | démarre un nouveau cas (le premier |, qui suit le with, est optionnel). Le dernier cas, avec _, est toujours vérifié: il faut le mettre en dernier, car OCaml examine les cas dans l'ordre.
En fait on utilise en général les définitions par cas pour des fonctions qui portent sur des données structurées, car on peut en même temps déstructurer la donnée.
La fonction suivante renvoie true si le point p qu'on lui passe en paramètre est situé sur l'axe des
abscisses ou sur celui des ordonnées
let est_sur_un_axe p = match p with
(0., y) -> true
| (x, 0.) -> true
| _ -> false
Chaque cas est identifié par un motif auquel on associe un traitement.
Le motif peut contenir des constantes explicites (0,0.,"zero", etc) ou des variables de motif, comme x et y ci-dessus. Ces variables de motif sont locales: elles n'"existent" que durant le traitement associé au motif.
Avec des listes, on peut écrire des motifs qui utilisent [...] et ::.
let rec sum li = match li with
| [] -> 0 (* le "neutre" de + *)
| tete::queue -> tete + sum queue
let rec maximum li = match li with
| [] -> -. infinity (* le "neutre" de max *)
| [x] -> x (* cas de base, on pourrait l'omettre car max x (-. infinity) = x *)
| head::tl -> max head (maximum tl) (* <- liste de longueur >=2 *)
Notez que le cas _ n'est pas obligatoire! Il aurait été inutile au-dessus, car toute liste est soit de la forme [], soit de la forme head::tail.
Dans une définition par cas, l'essentiel est de bien couvrir tous les cas. L'une des grandes forces d'OCaml est qu'il vous aide à ne pas en oublier. Par exemple, si on avait oublié le cas de base dans la définition de maximum précédente, on aurait eu droit à un avertissement.
let rec maximum li = match li with
| [x] -> x
| head::tl -> max head (maximum tl)
Listes et complexité¶
Nous allons maintenant re-programmer les fonctions les plus usuelles sur les listes. Il faudra bien comprendre à la fois leur fonctionnement et leur complexité en temps pour savoir les utiliser à bon escient!
| Fonction | Complexité | Description |
|---|---|---|
List.append l1 l2 |
$\mathcal O(n_1)$ | concaténation |
List.length l |
$\mathcal O(n)$ | longueur |
List.mem x l |
$\mathcal O(n)$ | présence (membership) |
List.rev l |
$\mathcal O(n)$ | miroir |
Longueur d'une liste (List.length)¶
let rec length l = match l with
| [] -> 0
| hd::tl -> 1 + length tl
que l'on peut aussi écrire, sous une forme plus stylisée
let rec length = function
| [] -> 0
| _ :: tl -> 1 + length tl
On peut toujours remplacer let f x = match x with ... par la construction let f = function ....
Le mot-clé function permet de définir des fonctions anonymes, comme lam x: ... en Python.
Nous aurons l'occasion d'en reparler...
Étudions maintenant la complexité de notre fonction length. Si la liste l est de longueur $n$, on fera $n$ appels récursifs; chaque appel récursif prend un temps constant (le temps de sommer deux entiers).
On a donc une complexité en temps en $\mathcal O(n)$, autrement dit une complexité en temps linéaire.
Il ne s'agit pas ici de rentrer dans la définition exacte de cette notion, vous reverrez cela un peu plus sérieusement dans un cours d'algorithmique et très sérieusement dans un cours de calculabilité.
Présence dans une liste (List.mem)¶
Voyons maintenant comment définir par cas la fonction mem x l qui renvoie true si x est l'une des valeurs de l.
let rec mem x = function
| [] -> false (* CAS DE BASE : la liste vide ne peut pas contenir x *)
| head :: tail -> (* SI LA LISTE N'EST PAS VIDE *)
if x = head (* soit x apparait en tête de liste *)
then true
else mem x tail (* soit x apparait dans la queue de la liste *)
Complexité $\mathcal O(n)$, puisque dans le pire cas on fait $n$ appels récursifs.
let rec mem x = function (* équivalent, mais écrit plus compact *)
| [] -> false
| hd::tl -> x=hd || mem x tl
Le deuxième cas, hd::tl, contient deux sous-cas. Faisons-les remonter pour avoir une définition par cas avec 3 cas.
Nous allons utiliser le mot-clé when
let rec mem x = function
| [] -> false
| head::_ when head = x -> true (* <- notez le *when* *)
| _::tail -> mem x tail
Vous pourriez être tentés de remplacer le deuxième cas par x::_, mais ça ne marche pas.
let rec mem x = function
| [] -> false
| x::_ -> true
| _::tail -> mem x tail
Le motif x::_ signifie "appelons désormais x le premier élément de la liste". On est en train de (re)définir localement la variable x en lui donnant pour valeur celle de la tête de li.
Du coup, OCaml nous avertit que le dernier cas _::tail est inutile. Et en effet, il est entièrement couvert par le précédent, x::_, qui englobe toute liste de longueur non nulle.
L'accès à la $n$ième valeur de la liste (List.nth)¶
let rec nth l n = match (l, n) with
| (x::_, 0) -> x
| (_::tl, i) -> nth tl (i-1)
| ([], _) -> invalid_arg "erreur dans nth n l : n<0 ou n>length l."
La fonction invalid_arg permet de terminer la fonction en faisant une erreur avec un message d'explication. Si l'on ne veut pas avoir un avertissement d'OCaml, il faut bien traiter ce troisième cas d'une façon ou d'une autre!
nth [1;2;3] 2
nth [1;2;3] 3 (* en fait, invalid_arg "lève une exception" *)
Concaténation de listes (List.append)¶
let rec append l1 l2 = match l1 with
| [] -> l2
| x::tl -> x::append tl l2
COMPLEXITÉ : $\mathcal O(n)$, et oui... on verra comment faire un temps constant avec des listes mutables, mais avec des listes non mutables, on ne peut pas espérer mieux.
Image miroir d'une liste (List.rev)¶
let rec rev = function
| [] -> []
| hd::tl -> (rev tl) @ [hd]
Regardons de près la complexité de rev.
On doit faire $n$ appel récursifs, et au cours d'un appel récursif il faut faire un append, qui prend un temps $\mathcal O(|tl|)$.
Le temps total est donc, à un facteur prêt
$$n+(n-1)+\cdots+2+1= \frac{n(n+1)}{2}$$soit une complexité en $\mathcal O(n^2)$.
On peut faire mieux!
D'ailleurs, la fonction List.rev de la librairie standard est de complexité $\mathcal O(n)$.
Pour cela, il va falloir s'interdire d'utiliser @ ou List.append... Une idée?
L'astuce consiste à généraliser le problème: nous allons nous intéresser à la fonction rev_append l1 l2, qui concatène l2 à l'image miroir de l1
List.rev_append [1;2;3] [4;5;6]
Re-programmons maintenant cette fonction rev_append.
let rec rev_append l1 l2 = match l1 with
| [] -> l2
| hd::tl -> rev_append tl (hd::l2)
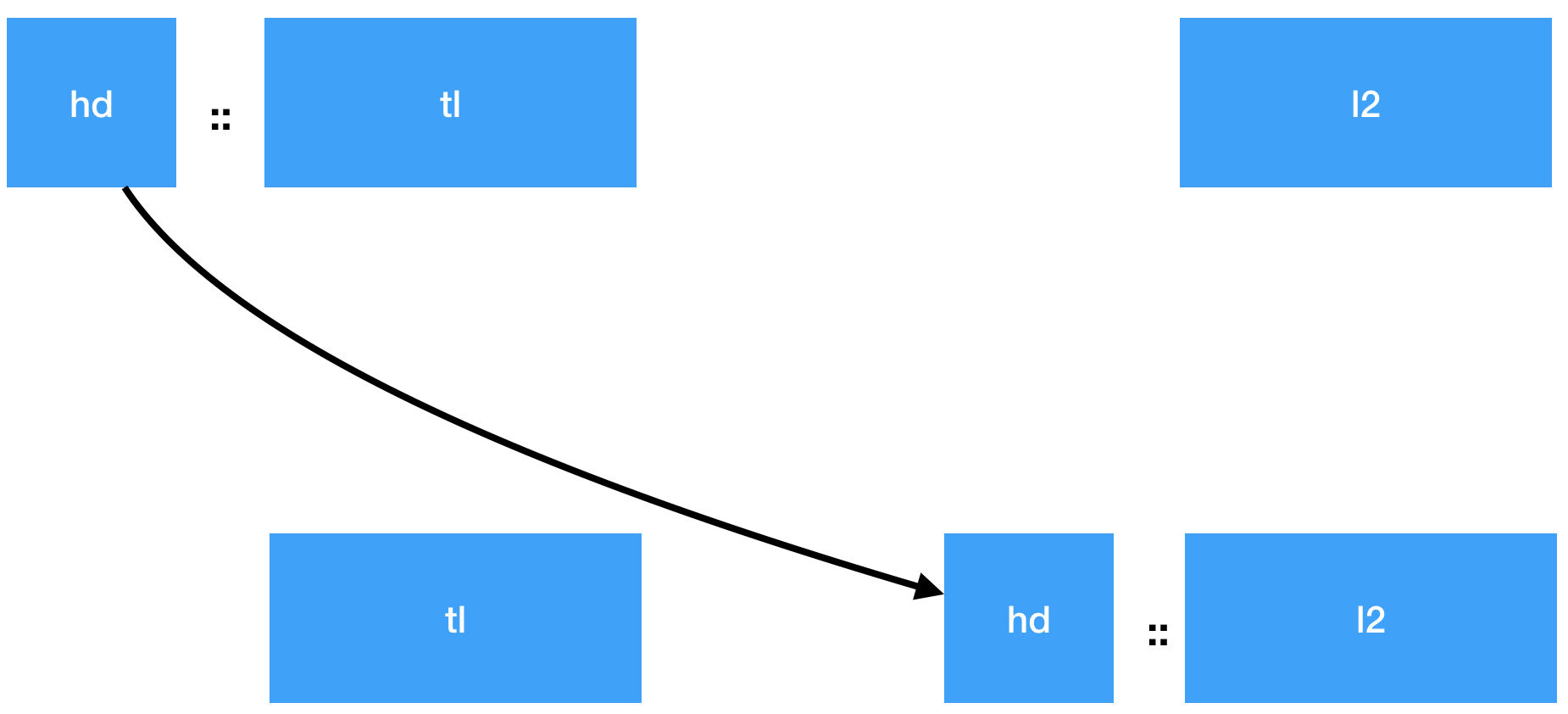
À partir de rev_append, on peut définir la fonction rev assez facilement. Et cette fois-ci, on obtient bien une complexité en $\mathcal O(n)$.
let rev l1 = rev_append l1 []
Comment utiliser List.sort?¶
La fonction List.sort permet de trier une liste. Elle attend deux arguments:
- une fonction pour savoir sur quel critère trier la liste
- la liste à trier
Si l'on veut trier avec le critère "standard", on peut utiliser la fonction compare de la librairie standard
(* ordre croissant sur les entiers *)
List.sort compare [3;2;1;4]
(* ordre alphabétique croissant *)
List.sort compare ["un"; "zèbre"; "pourchasse"; "le"; "lyon"]
(* ordre lexicographique croissant *)
List.sort compare [(1,1); (2,1); (1,3); (2,2)]
compare (* le type de la fonction compare de la librairie standard est : *)
Pour changer le critère de tri, il faut fournir la bonne fonction de comparaison.
Une fonction de comparaison cmp pour trier une 'a list doit avoir le type
cmp:'a -> 'a -> int.
cmp x y renverra
- $1$ si x est strictement plus grand que y (au sens de cmp)
- $-1$ si y est strictement plus grand que x
- $0$ sinon (x et y sont "équivalents").
Quelques exemples de fonctions de comparaison
let decroissant x y = (* decroissant x y = compare y x *)
if x < y then 1 else if x > y then -1 else 0
in List.sort decroissant [1;2;3;4]
let norme2 (x,y) = x**2. +. y**2.
(* le tri par rapport à la norme *)
let cmp v1 v2 = compare (norme2 v1) (norme2 v2) in
List.sort cmp [(-. 1., -. 1.); (1., 1.); (0., 0.); (0.5, 2.)]
On préfèrera parfois la fonction List.stable_sort qui laisse deux éléments "équivalents" dans l'ordre dans lequel ils se trouvent dans la liste de départ.
Avec sort, il est possible d'intervertir deux éléments qui sont équivalents (par exemple (1,1) et (-1,-1) dans l'exemple précédent).
Il y aussi une fonction List.fast_sort qui est plus rapide.
Application : un algorithme de recommandation¶
Nous allons maintenant écrire un algorithme de recommandation pour une compagnie qui vend des bonbons en ligne.
Cette compagnie propose deux produits, des bonbons bleus et des bonbons rouges. Notre but est de recommander à un nouveau client un bonbon de la bonne couleur en devinant celle qu'il préfère à partir de son profil.
Pour cela, on cherche d'anciens clients ayant un profil similaire et on se base sur leur préférence pour deviner.
Pour faire simple, un profil est un couple de flottants (age, revenu). On a donc un nuage de points du plan rouges ou bleus qui correspondent aux profils des anciens clients.
let nuage = [(13., 50., "bleu"); (80., 2000., "rouge"); (19., 400., "bleu") (* etc *)]
Notre algorithme de recommandation sera très simple: pour calculer la couleur au point p, on va déterminer la couleur majoritaire parmi les trois points les plus proches de p dans le nuage.
let recommande nuage (age, revenu) =
let dist (age', revenu', couleur) = norme2 (age' -. age, revenu' -. revenu) in
let cmp p1 p2 = compare (dist p1) (dist p2) in
match List.sort cmp nuage with
| _::(_,_,c2)::(_,_,c3)::_ when c2=c3 -> c2
| (_,_,c1)::_ -> c1
| _ -> invalid_arg "le nuage doit contenir au moins 1 point"
Et voilà!
Allez, pour finir, nous allons représenter le nuage de points dans une fenêtre graphique et utiliser la souris pour sélectionner le profil à deviner.
Illustration : introduction à la librairie Graphics¶
Commençons par un petit dessin
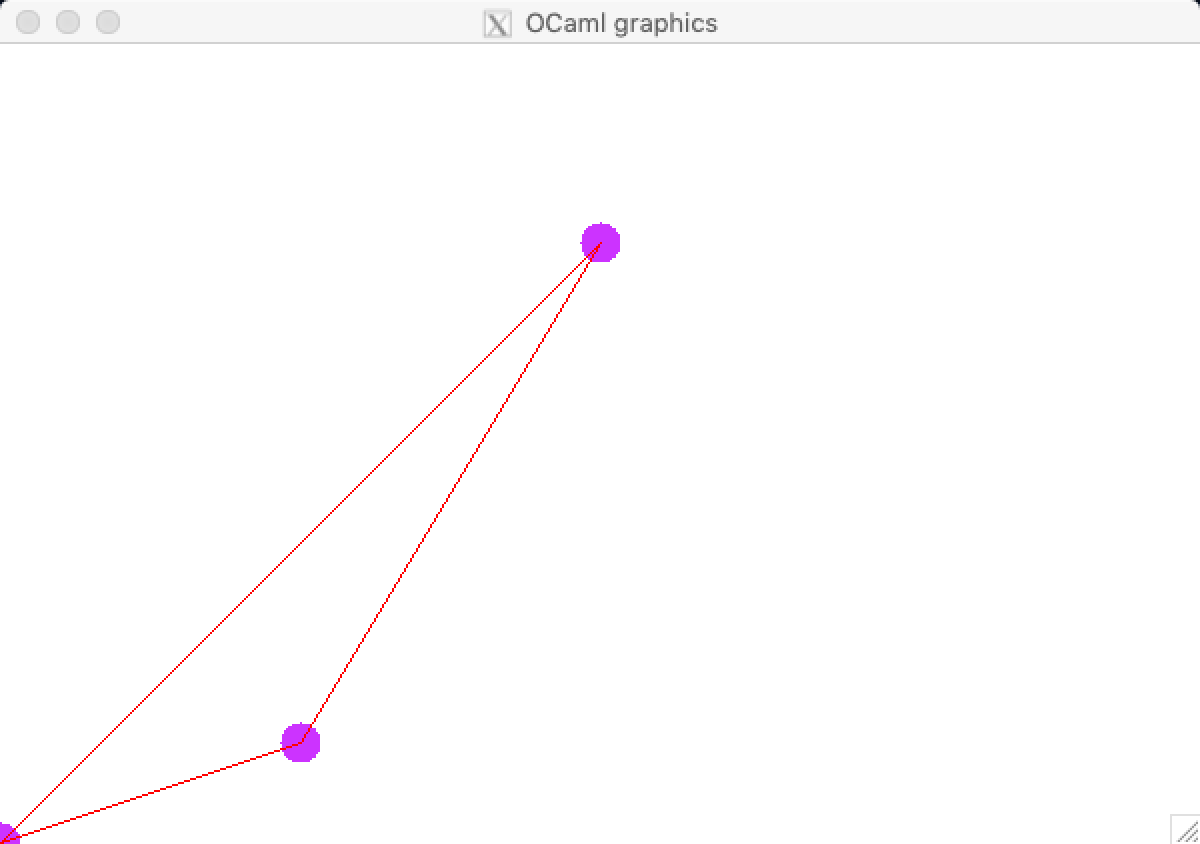
#load "graphics.cma";; (* <- au toplevel uniquement: pour "charger" le module *)
open Graphics;; (* from Graphics import *, si on était en Python *)
let () = begin
open_graph " 600x400"; (* crée une nouvelle fenêtre 600 sur 400 *)
(* NOTE : faites attention à l'espace devant 600 et au x minuscule *)
(* Graphics risque de bouder si vous les oubliez! *)
set_color 0xcc33ff; (* code RGB de la couleur en hexadecimal, ici violet *)
fill_circle 0 0 10; (* dessine un cercle plein en bas à gauche de rayon 10 *)
fill_circle 300 300 10;
fill_circle 150 50 10;
set_color red;
moveto 0 0; (* déplace la "tortue" en (0,0) sans tracer *)
lineto 300 300; (* déplace la "tortue" en (300,300) en traçant *)
lineto 150 50;
lineto 0 0 (* <- pas de ; après la dernière instruction *)
end
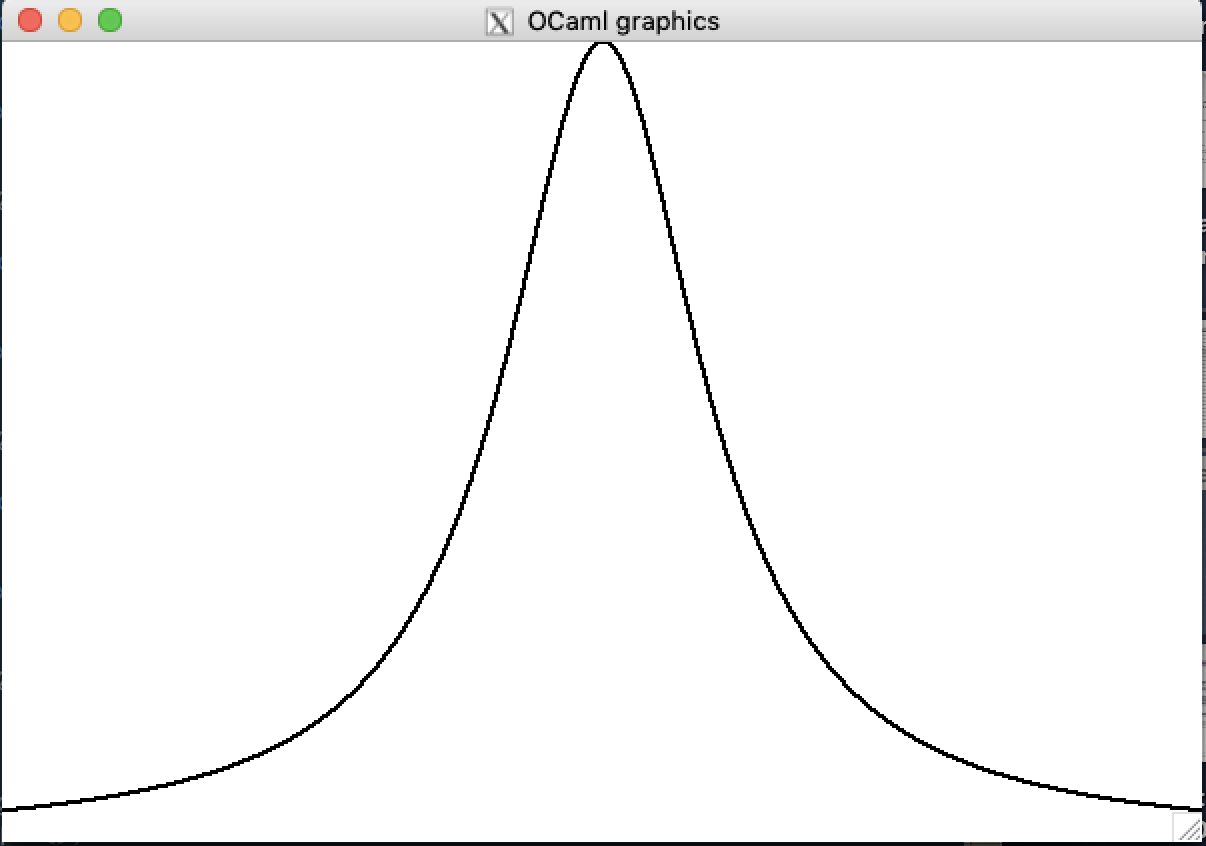
Comment tracer le graphe d'une fonction?¶
On va discrétiser la fonction $f:\mathbb{R}\to\mathbb{R}$ à tracer.
Les coordonnées dans le canevas d'OCaml sont entières, et on veut tracer une fonction flottante. Il faut donc la transformer en une fonction $g:\mathbb{N}\to\mathbb{N}$
let discretise f x = int_of_float (f (float_of_int x))
Pour le tracé proprement dit, on va se placer en (0,f(0)), puis on avance en (1,f(1)), puis (2,f(2)), etc.
let trace f =
let f = discretise f in
let rec trace_depuis x = begin
lineto (x+1) (f (x+1));
if x = size_x() then () (* si on est arrivé au bord droit, on s'arrête *)
else trace_depuis (x+1) (* sinon on continue le tracé en partant de x+1 *)
end
in begin
moveto 0 (f 0);
trace_depuis 0
end
let f x = 400. /. (1. +. (x /. 60. -. 5.) ** 2.)
let () = trace f
Comment générer un nuage de points?¶
On va simplement tirer 100 points au hasard: s'ils sont au-dessus de la courbe, ils sont bleus, sinon ils sont rouges.
let couleur_point (x,y) =
if f x > y then red else blue
let tire_point () =
let (x, y) = (Random.float 600., Random.float 400.)
in (x, y, couleur_point(x, y))
let rec tire_nuage_de_points = function
| 0 -> []
| n -> tire_point() :: tire_nuage_de_points (n-1)
let nuage = tire_nuage_de_points 100
Comment dessiner un nuage de points?¶
Par récurrence! On commence par dessiner un point
let dessine_point(x,y,c) = begin
set_color c;
fill_circle (int_of_float x) (int_of_float y) 5
end
Puis par récurrence on parcours la liste des points et on les dessine un à un.
let rec dessine_nuage = function
| [] -> () (* rien à dessiner! *)
| p::tl -> begin dessine_point p; dessine_nuage tl end
let () = dessine_nuage nuage
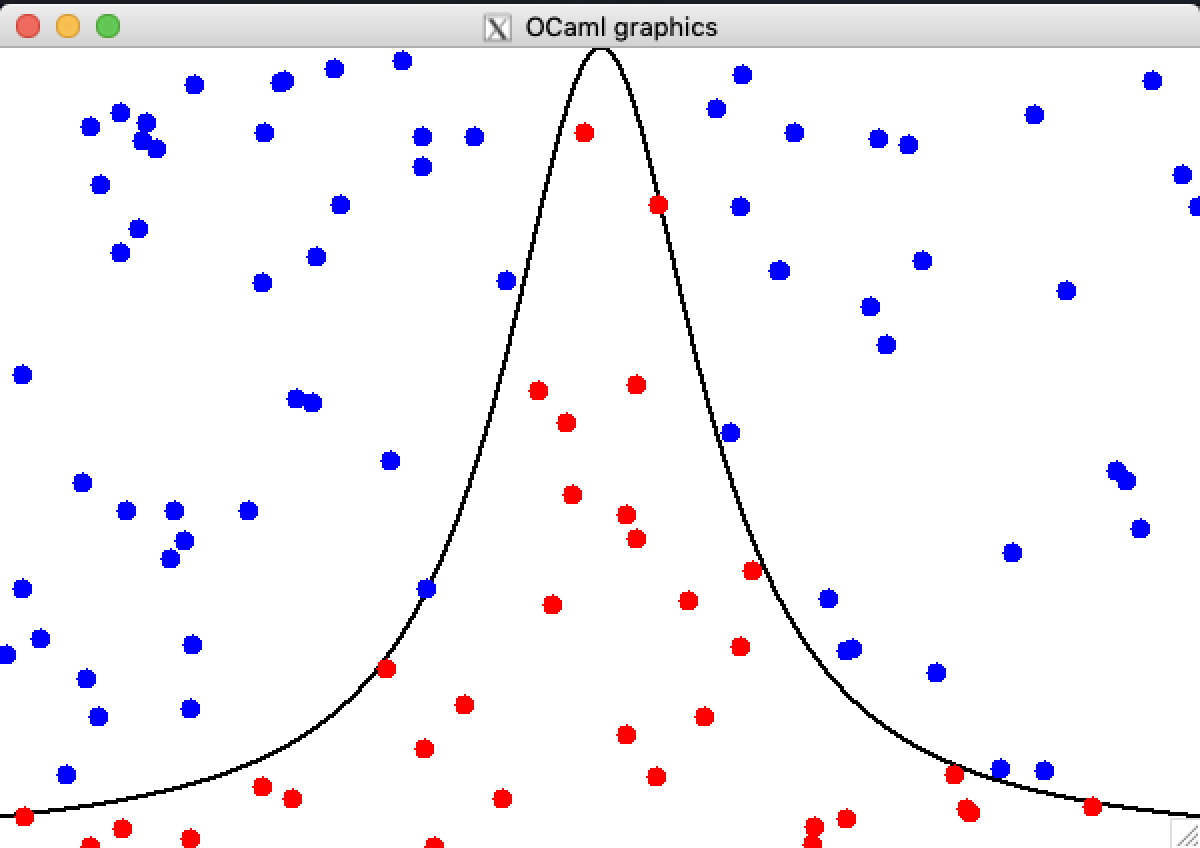
OCaml propose aussi une fonction d'itération List.iter (c'est une fonction d'ordre supérieur, cf prochains cours)
List.iter f [a1;a2;...;an] est équivalent à
begin f a1;f a2;...;f an end.
On peut donc écrire dessine_nuage plus simplement.
let dessine_nuage nuage = List.iter dessine_point nuage
(* ou plus simplement *)
let dessine_nuage = List.iter dessine_point
Comment tester l'algorithme de recommandation?¶
On va récupérer la position de la souris et dessiner un point à l'endroit où elle se trouve, en se basant sur notre algorithme de recommandation pour déterminer sa couleur.
Il faudra tout redessiner chaque fois que la souris bouge.
let redessine _ = begin
clear_graph (); (* effacer tous les dessins *)
trace f; (* tracer la courbe en cloche, la "frontière" à deviner *)
dessine_nuage nuage; (* dessiner les points connus *)
let (x,y) = mouse_pos () in (* recuperer la position de la souris *)
let (x,y) = ((float_of_int x),(float_of_int y)) in
let c = recommande nuage (x,y) in (* calculer la couleur recommandée en ce point *)
dessine_point(x,y,c) (* dessiner ce nouveau point*)
end
Il ne reste plus qu'à installer la fonction de dessin dans la boucle infinie de Graphics, et demander à l'appeler à chaque fois que la souris est déplacée.
let () = begin
open_graph " 600x400";
loop_at_exit [Mouse_motion] redessine (* similaire à quelque chose comme *)
(* while true do begin wait_mouse(); redessine() end;*)
end