Les données structurées et la programmation fonctionnelle¶
Au second cours, nous avons étudié les listes chaînées, un premier exemple de structures de données récursives. Nous allons approfondir dans ce cours la notion de structure de données récursives et aborder les arbres.
Mais avant cela, nous allons voir comment structurer des données à l'aide des enregistrements et des énumérations.
Les enregistrements¶
Reprennons l'exemple des points colorés de l'algorithme de recommendation du cours précédent. Nous avions représenté chaque point coloré par un triple (x,y,c). Si p est un point coloré, on peut copier sa couleur dans une variable c en écrivant let (_,_,c) = p in ....
Ce n'est pas toujours très pratique, en particulier il faut se souvenir que la couleur est à la troisième position. Quand on passe à des données structurées de plus grandes dimensions, on préfère utiliser des enregistrements (record en anglais) pour grouper les données ensemble.
type point_colore = {x:int; y:int; c:string}
let p1 = {c="rouge"; x=0; y=0}
let p2 = {y= 0; x=22; c="bleu"}
L'étape de déclaration du type est essentielle: elle permet à OCaml de savoir que x, y et c sont des identifiants de champs du type point_colore. Elle permet ainsi à OCaml d'éviter les définitions de point colorés incomplètes ou mal typées
let p3 = {x=0; y=0}
let p4 = {x=0; y=0; c=0}
let p5 = {x=0; y=0; color="bleu"}
On accède à un champs d'un enregistrement avec la notation .
p1.c
Prenons un autre exemple: créons un enregistrement pour représenter un nombre complexe
type complexe = {re:float; im:float}
let plus_complexe z1 z2 = {
re = z1.re +. z2.re;
im = z1.im +. z2.im
}
On peut créer une copie d'un enregistrement r en modifiant certains champs seulement, et en laissant les autres inchangés. On écrit {r with ...} en précisant les valeurs des champs qui changent.
let conjugue z = {z with im = -. z.im }
conjugue {re=13.; im=5.}
On peut déconstruire un tuple dans une définition ou un motif et récupérer ainsi certains champs.
let norme {re=r; im=i} = r ** 2. +. i ** 2.
(* on peut utiliser les champs comme des noms de variables *)
let norme {re; im} = re ** 2. +. im ** 2.
let est_rouge_ou_bleu p = match p with
| {c = "rouge"; x = _ ; y = _ } -> true
| {c = "bleu"; x = _ ; y = _ } -> true
| _ -> false
On n'est pas obligé de lister tous les champs dans un motif.
De plus, dans une définition par cas, on peut regrouper plusieurs motifs et leur associer un seul et même traitement.
La définition précédente peut donc se simplifier.
let est_rouge_ou_bleu p = match p with
| {c = "rouge"} | {c = "bleu"} -> true
| _ -> false
Bien choisir les noms des champs¶
Souvent vous aurez plusieurs types d'enregistrements qui coexisteront dans votre programme.
Pour qu'ils vivent en bonne entente, il vaut mieux que leurs noms de champs soient bien distincts (au moins en attendant de voir les modules pour mettre un peu d'ordre dans tout ça).
Par exemple, si on avait réutilisé les noms x et y dans la définition du type complexe, on aurait perturbé l'usage des points colorés, de type {x:int; y:int; c:string}.
type complexe2 = {x:float; y:float}
let p6 = {x = 1; y = 1; c = "jaune"} (* le champs c sauve la mise ici *)
let ramene_a_0 p = {p with x=0; y=0} (* sans le champs c, OCaml infère p:complexe *)
Lorsque l'inférence de type d'OCaml n'est pas satisfaisante, on peut déclarer le type que l'on attend pour une variable ou une expression. OCaml ne l'acceptera pas les yeux fermés, mais il en tiendra compte.
let app g x : int = g x (* je demande à ce que app g x soit de type int *)
let app g (x:int) = g x (* je demande à ce que x soit de type int *)
(* je demande à OCaml d'inférer un type à ramene_a_0 tel que le type de p soit point_colore *)
let ramene_a_0 (p:point_colore) = {p with x=0;y=0}
(* je demande à OCaml d'inférer un type à ramene_a_0 tel que le type de la valeur retournée soit point_colore *)
let ramene_a_0 p = ({p with x=0;y=0} : point_colore)
Rajouter des opérateurs au langage¶
Supposons que l'on veuille calculer la somme de deux nombres complexes z1 et z2. On peut appeler la fonction plus_complex décrite précédemment et écrire plus_complexe z1 z2. C'est tout de même un peu lourd, et OCaml propose mieux: introduire un nouvel opérateur dans le langage!
let (++) z1 z2 = {re = z1.re +. z2.re; im= z1.im +. z2.im}
let z1 = {re=1.; im=0.}
let z2 = {re=0.; im=1.}
let z3 = z1 ++ z2
En interne, ++ n'est rien d'autre qu'une fonction qui prend deux paramètres (c'est la fonction plus_complexe de tout à l'heure). Lorsqu'on parle de la fonction toute seule, on écrit (++), et lorsqu'on l'applique à ses deux arguments, on l'écrit en notation infixe, entre les deux arguments.
Autre exemple: l'opérateur ^ ne permet pas de concaténer des caractères et des chaînes de caractères
'a' ^ "bcd"
Qu'à cela ne tienne, définissons de nouveaux opérateurs pour faire des concaténation "mixtes" qui convertissent le caractère en chaîne de caractères (fonction Char.escaped )
let (^::) c s = (Char.escaped c) ^ s
let (^@) s c = s ^ (Char.escaped c)
let chaine1 = 'a' ^:: "bcd"
let chaine2 = "abc" ^@ 'd'
Les possibilités sont infinies... vous pourrez vous amuser à étendre le langage comme bon vous semble, il faudra seulement prendre garde à utiliser des caractères spéciaux pour définir vos opérateurs infixes, et à respecter quelques règles.
On peut aussi définir des opérateurs unaires préfixe, comme - ou -..
Leur nom devra commencer par !, ?, ou ~ et ne comporter que des caractères spéciaux.
let (~~) z = { z with im = -. z.im } (* un opérateur unaire pour le conjugé *)
let i = {re=0.; im=1.} in ~~ (i ++ i)
OCaml applique des règles d'associativité sur les opérateurs définis par l'utilisateur qui se basent sur le premier caractère spécial utilisé. Par exemple, *** est prioritaire sur ++, qui est prioritaire sur ====, etc.
Enfin, on a le droit de redéfinir des opérateurs "prédéfinis". Pour ne pas les perdre définitivement, mieux vaut tout de même redéfinir localement et non globalement (en pratique, on fait ça plutôt avec des modules).
let (+) {re = x1; im = y1} {re = x2; im = y2} = {
re = x1 +. x2;
im = y1 +. y2;
}
in let ( * ) {re=x1; im=y1} {re=x2; im=y2} = {
re = x1 *. x2 -. y1 *. y2;
im = x1 *. y2 +. x2 *. y1
}
in let i = {re = 0.; im = 1.}
in i + i * i + i (* égal à i + (i*i) + i *)
Les types énumérés¶
Certaines valeurs peuvent parfois se présenter sous plusieurs formes. Par exemple, une couleur peut être définie par
- un nom de couleur (ex:
"red","green","blue", ...) - trois entiers 8 bits en mode RGB (ex:
(255, 255, 0)pour jaune=rouge+vert) - un entier 32 bits en mode CYMK (cyan, magenta, yellow, black)
- trois entiers 8 bits en mode HSL (hue, saturation, lightness)
- ...
Si l'on veut écrire une fonction qui prend en argument une couleur, il peut être intéressant de prévoir tous ces cas. C'est ce que permet de faire un type énuméré.
type couleur =
| ParNom of string
| RGB of int * int * int
| CYMK of int
| HSL of int * int * int
Cette déclaration de type introduit des constructeurs pour le type couleur. Chaque valeur du type couleur est "étiquetée" par un constructeur.
Règle d'or de la syntaxe des constructeurs¶
Un contructeur de type commence nécessairement par une majuscule
Comme leur nom l'indique, les constructeurs permettent de construire des valeurs du type couleur.
let noir1 = ParNom "black"
let noir2 = RGB(0,0,0) (* aucune couleur mélangée *)
Attention, noir1 est de type couleur, mais pas du type string.
String.length noir1
C'est comme si chaque constructeur était une fonction "injective" vers le type couleur. En math, on noterait
Voyons d'autres exemples de définition de couleur.
let noir3 = CYMK 0x000000ff (* 8 bits de poids faible = 255 *)
let noir4 = HSL(42,111,0) (* luminosité = 0 *)
On peut maintenant écrire une fonction qui prend un argument de type couleur et qui renvoie un résultat qui dépend du contructeur de type qui a été utilisé.
let est_noir c = match c with
| ParNom "black" | RGB(0, 0, 0) | HSL(_,_,0) -> true
| CYMK x when x mod 256 = 255 -> true
| _ -> false
On pourrait redéfinir les booléens avec des constructeurs "sans arguments", ou plutôt de type unit.
type booleens =
| Vrai of unit
| Faux of unit
Vrai () = Faux () (* faux, car même si () = (), l'étiquette est différente *)
OCaml prévoit cet usage particulier des constructeurs "sans argument", bien utile pour décrire un ensemble fini de valeurs. On les écrit tout simplement "sans argument".
type jour = Lundi | Mardi | Mercredi | Jeudi | Vendredi | Samedi | Dimanche
Le type 'a option¶
Le type 'a option est un type prédéfini. Cependant, pour expliquer comment il fonctionne, rien de tel que le redéfinir.
type 'a option_ =
| None
| Some of 'a
Ce type énuméré est couramment utilisé pour la valeur renvoyée par une fonction qui n'est pas définie pour tous les paramètres.
let racine_carree x = if x < 0. then None else Some (sqrt x)
C'est aussi un type qui permet d'avoir la valeur None comme "bouche-trou" dans une structure de données
type etat_civil = {
annee_naissance : int;
annee_deces : int option
}
let jacques = {annee_naissance = 1932 ; annee_deces = Some 2019}
let valery = {annee_naissance = 1926; annee_deces = None}
Les types polymorphes¶
Le type 'a option est paramétrique en la variable de type 'a. C'est un type polymorphe, de même que le type 'a list.
Comme on vient de le voir, il est possible de définir un type polymorphe, il suffit d'introduire la variable de type juste après le mot-clé type. On peut par exemple définir une "matrice" de valeurs de type 'a comme une liste de listes de valeurs de type 'a.
type 'a matrice = 'a list list (* pour l'exemple, en pratique à éviter *)
Si on veut une matrice "infinie dénombrable", on pourra la représenter par une fonction
type 'a matrice = int * int -> 'a (* m (i,j) renvoie la valeur ligne i et colonne j *)
Si on veut une définition générale de matrice, finie ou infinie, on peut considérer que les indices de lignes et de colonnes sont pris dans des "ensembles" qui sont eux-mêmes des paramètres.
type ('a, 'ligne, 'colonne) matrice = 'ligne * 'colonne -> 'a
Notez que si le type paramétré que l'on définit prend plusieurs paramètres, on les met entre parenthèses.
Les types récursifs¶
Un type récursif est un type qui est défini à partir de lui-même. Le type 'a list est un type récursif: pour s'en convaincre, essayons de le redéfinir.
type 'a liste =
| Empty (* Empty <=> [] *)
| Cons of 'a * 'a liste (* Cons(hd,tl) <=> hd::tl *)
On a bien besoin du type 'a liste pour décrire les arguments de Cons!
Par contre, contrairement aux définitions de fonctions récursives, inutile de rajouter le mot-clé rec pour une définition de type récursive.
let hd l = match l with
| Empty -> invalid_arg "liste vide!"
| Cons(x,tl) -> x
On peut aussi définir simultanément plusieurs types mutuellement récursifs. Le mot-clé essentiel pour des définitions mutuellement récursives est and.
L'exemple ci-dessous est une autre définition des listes chaînées proche de celle qu'on ferait en C.
type 'a cell = {hd:'a; tl:'a liste}
and 'a liste = 'a cell option (* <- il faut lire ('a cell) option *)
let empty = None
let cons hd tl = Some {hd=hd; tl=tl}
Notez dans le type inferré de cons qu'OCaml écrit indifféremment 'a liste et 'a cell option. Ces deux expressions de type s'évaluent en un seul et même type.
'a liste $\Leftrightarrow$ 'a cell option
Notez aussi le type de empty: 'a option $\Rightarrow$ 'a liste.
Il n'est pas très commode du point de vue du programmeur d'avoir plusieurs expressions de type qui parlent du même type. Ceci ne se produit pas avec les types récursifs basés sur des constructeurs et une énumération, aussi on privilégie en général les définitions de type récursives basées sur des types énumérés.
D'ailleurs, pour des raisons d'efficacité de l'inférence de type, OCaml ne permet pas par défaut d'écrire tous les types récursifs que l'on voudrait.
type 'a liste = ('a * 'a liste) option
Il est possible de demander à OCaml d'utiliser l'algorithme d'inférence de type qui sait traiter les types récursifs comme celui-ci. Pour cela, on doit lancer ocaml ou ocamlc avec l'option -rectypes. Cette option est d'un usage assez rare, car avoir des expressions de type différentes qui décrivent le même type introduit beaucoup de confusion. C'est cependant un aspect du langage qui fait l'objet de discussions au sein de l'équipe de développeurs d'OCaml, rien ne dit que les choses n'évolueront pas dans le futur.
Les arbres d'expression arithmétique¶
Définissons maintenant un type pour représenter les arbres d'expressions arithmétiques que l'on rencontre par exemple en calcul formel (voir cours de Python de L1!).
type arbre =
| Feuille of feuille
| Noeud of operateur * arbre * arbre
and feuille =
| Const of int
| Var of string
and operateur = PLUS | MULT | SUB | DIV
Note : pour des questions de présentation, on a utilisé le and des définitions mutuellement récursives, mais on aurait pu s'en passer en définissant les types dans l'ordre inverse, "bottom-up"...
Construire un arbre d'expression arithmétique¶
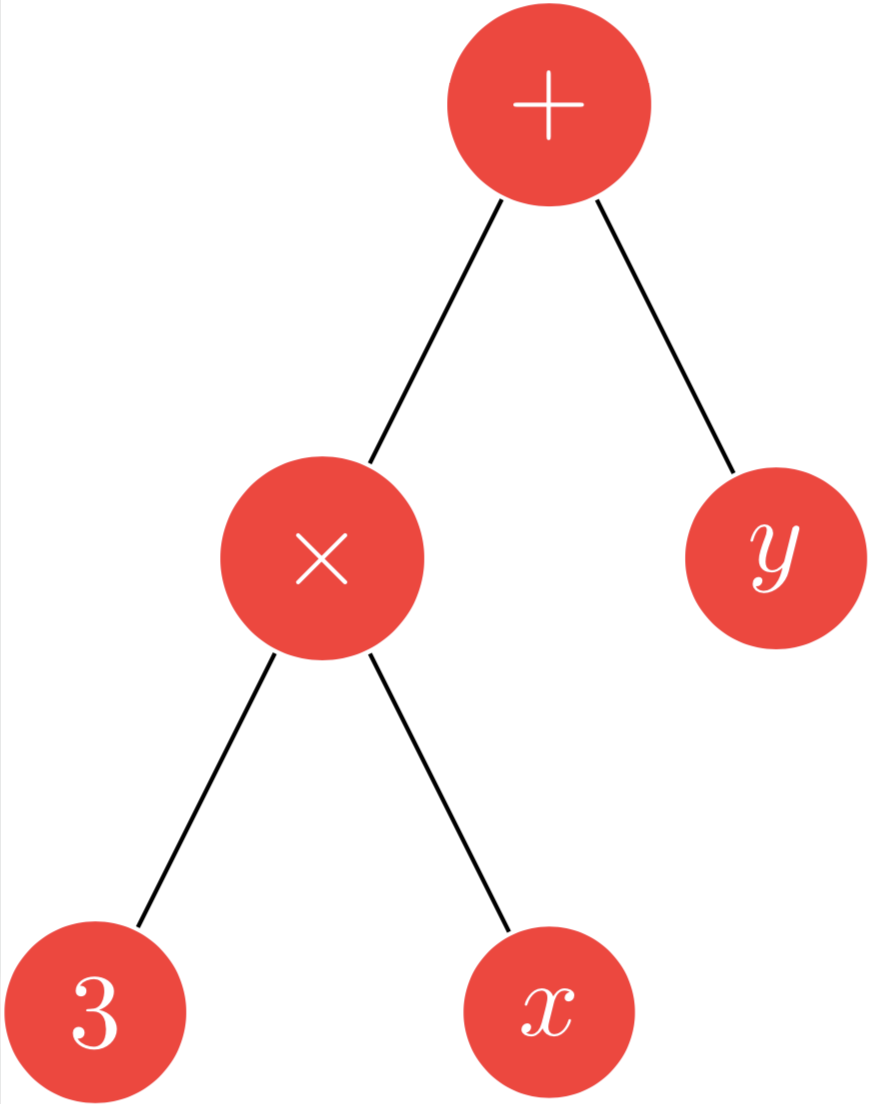
Définissons les arbres des expressions "$3\times x$" et "$(3\times x) + y$"
let arbre1 =
Noeud (MULT,
Feuille(Const 3),
Feuille(Var "x"))
let arbre2 = Noeud(PLUS,arbre1, Feuille(Var "y"))
Certes, c'est un peu lourd de devoir écrire tous ces constructeurs... on pourrait améliorer cela en introduisant de nouveaux opérateurs dans le langage (exercice!). Malgré tout, le résultat affiché n'est pas très lisible.
Afficher un arbre d'expression arithmétique¶
On va définir une fonction string_of_arbre : arbre -> string qui renvoie une
chaîne de caractères qui permette d'afficher "joliement" l'arbre qu'elle représente.
En anglais, on parle souvent de pretty-printing.
Pour définir string_of_arbre, on va procéder par récurrence et par études de cas, comme pour les listes de la semaine dernière, sauf que les motifs et le raisonnement se compliquent un peu...
let rec string_of_arbre = function
| Feuille(Const n) -> string_of_int n
| Feuille(Var x) -> x
| Noeud(op, ag, ad) ->
let strg = string_of_arbre ag
and strd = string_of_arbre ad
in let strop = match op with
| PLUS -> "+" | SUB -> "-" | MULT -> "*" | DIV -> "/"
in "(" ^ strg ^ strop ^ strd ^ ")"
string_of_arbre arbre2
On pourrait économiser quelques parenthèses, à condition de se creuser un peu la tête... c'est pourquoi je vous le laisse en exercice!
Au lieu d'économiser les parenthèses, on va surtout chercher à rendre le code de notre fonction
string_of_arbre plus lisible. C'est un exercice toujours utile à effectuer, un code lisible est un code sur lequel on peut plus facilement découvrir des erreurs.
Dans le cas présent, on a trois types, à savoir arbre, feuille et operateur; on a donc intérêt à avoir trois fonctions de pretty-printing.
let rec string_of_arbre = function
| Feuille f -> string_of_feuille f
| Noeud(op, ag, ad) ->
let strg = string_of_arbre ag
and strd = string_of_arbre ad
and strop = string_of_operateur op
in "(" ^ strg ^ strop ^ strd ^ ")"
and string_of_feuille = function
| Const n -> string_of_int n
| Var x -> x
and string_of_operateur = function
| PLUS -> "+" | SUB -> "-" | MULT -> "*" | DIV -> "/"
string_of_arbre arbre2
Petite astuce pour le travail dans un toplevel : on peut "installer" un pretty-printer pour un type t, de sorte que le toplevel adopte notre afficheur maison pour toutes les valeurs de type t.
arbre2 (* l'arbre avec tous les constructeurs... MIAM! *)
Pour installer un pretty printer, on commence par définir une fonction à deux arguments:
- un formateur qui est une sorte d'écrivain à qui on peut envoyer des ordres (on en reparlera)
- un deuxième argument qui est la valeur du type à afficher.
On demande ensuite au formateur d'afficher une chaîne de caractères qui correspond à celle calculée par notre pretty-printer.
let pp_arbre fmt arbre = Format.fprintf fmt "%s" (string_of_arbre arbre)
Une fois la fonction pp_arbre définie, on procède à son installation en appelant la macro #install_printer
#install_printer pp_arbre
arbre2
Evaluer un arbre d'expression sans variables¶
On voudrait maintenant programmer une petite calculette qui prend en entrée une expression arithmétique sans variable et qui calcule l'entier correspondant. Par exemple, si arbre est l'arbre de l'expression $1+(2\times3)$, eval arbre renverra $7$.
let rec eval = function
| Feuille(Const n) -> n
| Noeud(binop, ag, ad) -> begin
let n1 = eval ag and n2 = eval ad in
match binop with
| PLUS -> n1 + n2
| SUB -> n1 - n2
| MULT -> n1 * n2
| DIV -> n1 / n2
end
| _ -> invalid_arg "contient des variables!"
let arbre = Noeud(PLUS,Feuille(Const 1),Noeud(MULT,Feuille(Const 2),Feuille(Const 3)))
in eval arbre
À nouveau, essayons d'améliorer la lisibilité de notre fonction eval en introduisant une fonction d'évaluation eval_op pour les opérateurs. Mais que doit renvoyer eval_op PLUS?
Tout simplement, eval_op PLUS renvoie la fonction d'addition (+) : int -> int -> int!
let eval_op = function
| PLUS -> (+) | SUB -> (-) | MULT -> ( * ) | DIV -> (/)
let rec eval = function
| Feuille(Const n) -> n
| Noeud(op, ag, ad) -> eval_op op (eval ag) (eval ad)
| _ -> invalid_arg "contient des variables!"
eval (Noeud(PLUS,Feuille(Const 1),Feuille(Const 2))) (*1+2*)
Evaluer une expression avec des variables (1)¶
On voudrait maintenant évaluer une expression en remplaçant les variables qui y apparaissent par leur valeur. Par exemple, si l'on remplace $x$ par 1 et $y$ par 2, l'expression $(3\times x)+y$ s'évalue en l'entier 5.
Il y a deux données à prendre en compte
- l'arbre d'expression proprement dit, et
- l'environnement d'interprétation, autrement dit les valeurs que l'on souhaite donner aux variables.
Pour représenter l'environnement, on va utiliser une liste associative formée de couple "clé-valeur".
let env = [ ("x", 1); ("y", 2)]
Cette représentation n'est pas la seule qu'on aurait pu choisir. En Python on aurait utilisé sans doute un dictionnaire, autrement dit une table de hachage. Les tables de hachage sont plus efficaces que les listes associatives quand il commence à y avoir beaucoup de clés. Cependant, pour utiliser une table de hachage en OCaml il faut faire des mutations, on en reparlera la semaine prochaine...
Quelques mots sur les listes associatives¶
Les listes associatives sont d'usage très courant en OCaml, à tel point qu'une partie du module List
leur est consacrée. Regardons maintenant le fonctionnement de quelques une des fonctions sur les listes associatives.
List.mem_assoc "x" [ ("x", 1); ("y", 2)] (* teste si "x" est une clé de env *)
List.assoc "x" [ ("x", 1); ("y", 2)] (* renvoie la valeur associée à la clé "x" *)
List.assoc "z" [ ("x", 1); ("y", 2)] (* lève l'exception Not_found si la clé n'est pas présente *)
(* s'il y a plusieurs associations possibles, c'est celle en début de liste qui est retenue *)
List.assoc "x" [ ("x", 3); ("x", 1); ("y", 2)]
(* pour créer une nouvelle liste associative en retirant une association *)
List.remove_assoc "y" [ ("x", 1); ("y", 2); ("z", 3)]
List.assoc_opt "x" env, (* comme List.assoc, mais renvoie une option *)
List.assoc_opt "z" env
Evaluer une expression avec des variables (2)¶
Nous sommes maintenant prêts à rajouter le cas manquant dans notre fonction eval
let rec eval env = function (* <- notez le paramètre env *)
| Feuille(Const n) -> n
| Feuille(Var x) -> List.assoc x env
| Noeud(binop, ag, ad) -> eval_op binop (eval env ag) (eval env ad)
arbre1, env, eval env arbre1
eval [] arbre1 (* si une variable n'est pas trouvée, l'exception Not_found stoppe l'évaluation *)
On pourrait faire plus propre en utilisant List.mem_assoc ou List.assoc_opt... ou en rattrapant l'exception, on en reparlera.
Des arbres d'arité arbitraire et polymorphes¶
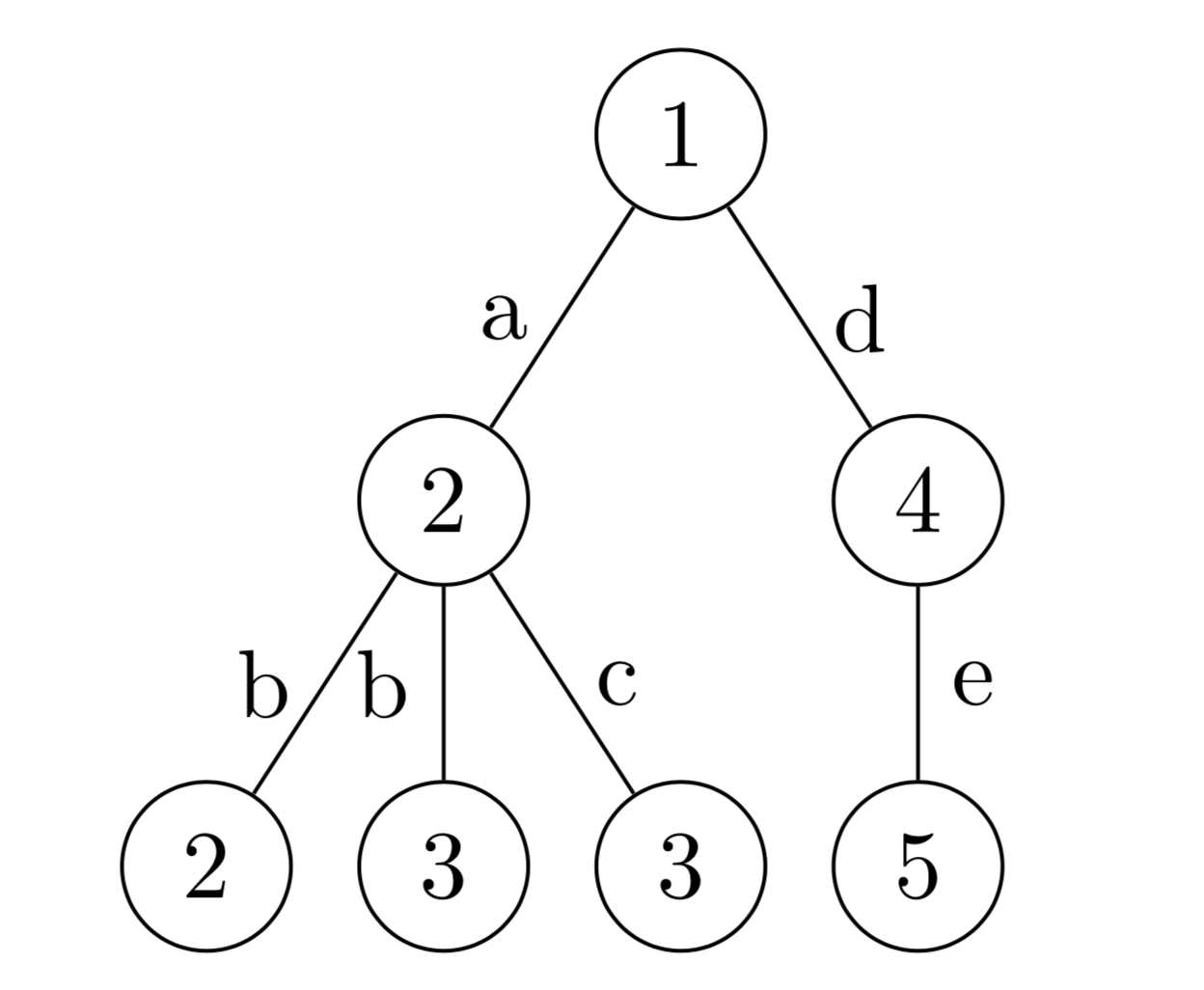
On va maintenant s'intéresser aux arbres d'arité arbitraire, dans lesquels le nombre de fils de chaque noeud n'est pas toujours le même. On va ajouter des "étiquettes" sur ces arbres à la fois sur les noeuds et sur les arètes. Nos arbres seront de plus polymorphes: les deux types d'étiquettes seront des paramètres.
type ('info_noeud, 'info_arete) arbre =
| Noeud of 'info_noeud * (('info_arete * ('info_noeud, 'info_arete) arbre) list)
let feuille x = Noeud(x, []) (* une feuille est un noeud sans fils *)
let fils x (Noeud(_ ,l)) = List.assoc x l (* renvoie le premier fils d'étiquette d'arête x *)
let arbre = Noeud(0, [('a', feuille 1); ('b', feuille 2)])
fils 'a' arbre
Application : les tries¶
Une trie$^*$, aussi appelé arbre préfixe, est une structure de données utilisée pour représenter une fonction de domaine fini de type
string -> 'a.
$^*$ le genre et la prononciation de ce "two-way anglicisme" ne fait pas l'unanimité.
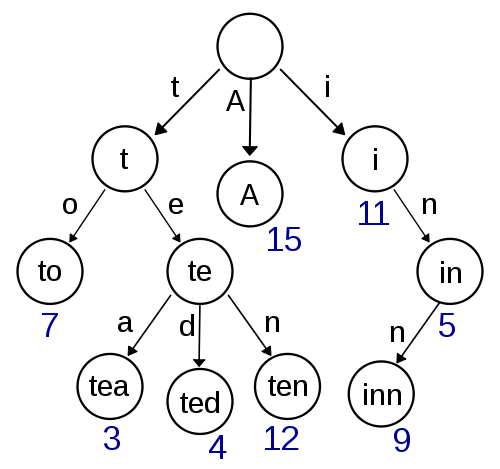
Ci-dessus: une trie pour l'association "to"$\mapsto7$, "tea"$\mapsto 3$, "i"$\mapsto 11$, ...
Étant donnée une clé s:string, on peut calculer la valeur associée en suivant la branche de l'arbre étiquettée par s. La valeur associée à s se trouve sur le noeud sur lequel la branche se termine.
Certains noeuds internes contiennent des valeurs, mais pas tous.
Pour représenter une trie, nous allons simplement utiliser un arbre, en prenant les caractères pour étiquetter les arètes
type 'a trie = ('a option, char) arbre
(* exemple : un trie avec une seule branche *)
let trie1 : int trie = Noeud(None, ['t',Noeud(None,['o',Noeud(Some 7,[])])]) (* "to"|-> 7 *)
Pour calculer la valeur associée à une clé, on va parcourir récursivement la trie.
À chaque étape, on doit lire un nouveau caractère de la clé. Ce caractère permet de trouver, à l'aide de la fonction fils, dans quel sous-trie continuer le parcours.
let rec assoc_opt cle trie =
match (String.length cle, trie) with
| 0, Noeud(v,_) -> v
| n, trie -> assoc_opt (String.sub cle 1 (n-1)) (fils cle.[0] trie)
(* String.sub : on met à jour la clé pour la suite du parcours
en retirant de la clé le caractère déjà lu *)
assoc_opt "to" trie1
Ce n'est pas idéal car String.sub fait une recopie de toute la chaîne à chaque fois. Pour éviter cela, je peux parcourir la chaîne de caractères cle avec une variable i=0,1,..., un peu comme une boucle for. Sauf que pour le moment je ne sais pas comment faire une boucle for en OCaml.
Solution: je crée une fonction auxiliaire f qui attend un entier i en paramètre; quand j'appelle f récursivement, il me suffit de lui passer i+1 en paramètre. Je passe aussi à f le sous-trie dans lequel je suis en train de chercher, que je modifie à chaque appel récursif comme dans la première version. Une fois f écrite, il me suffit de l'appeler avec les bonnes valeurs initiales: i=0, et strie=trie, le trie tout entier du début.
let assoc_opt cle trie =
let n = String.length cle in
let rec f i strie = match (i, strie) with (* <- ma fonction auxiliaire *)
| i, Noeud(v, _) when i = n -> v
| _ -> f (i+1) (fils cle.[i] strie)
in f 0 trie
assoc_opt "to" trie1