Programmation fonctionnelle¶

Semaine 7 : Modules et foncteurs¶

Etienne Lozes - Université Nice Sophia Antipolis - 2019¶

La notation . et les modules¶

Redéfinissons, pour l'exemple, une partie du module List.

In [2]:
module LList = struct
  type 'a llist = Empty | Cons of 'a cell
  and 'a cell = {hd: 'a; tl: 'a llist}
  let empty = Empty
  let cons x l = Cons {hd=x; tl=l}
  exception Empty_list
end
Out[2]:
module LList :
  sig
    type 'a llist = Empty | Cons of 'a cell
    and 'a cell = { hd : 'a; tl : 'a llist; }
    val empty : 'a llist
    val cons : 'a -> 'a llist -> 'a llist
    exception Empty_list
  end

Je pourrais définir la fonction hd à l'intérieur du module LList

module LList_possible = struct
  [...]
  let hd = function 
  | Empty -> raise Empty_list 
  | Cons cell -> cell.hd
  [...]
end

Mais je peux aussi vouloir définir la fonction hd à l'extérieur du module.

Comment faire?

Il me faut parler des constructeurs Empty et Cons, de l'exception Empty_list, qui sont définis dans l'espace de nom du module LList.

Comme je veux définir hd à l'extérieur du module LList, je n'ai pas accès directement à cet espace de nom, je dois utiliser la notation LList.

In [3]:
let hd = function
| LList.Empty -> raise LList.Empty_list
| LList.Cons cell -> cell.LList.hd
Out[3]:
val hd : 'a LList.llist -> 'a = <fun>

Chargement d'espaces de noms avec open et let open¶

Il est possible de charger l'espace de noms d'un module M en ajoutant open M. Toutes les définitions de M sont accessibles sans la notation M. dans la suite. C'est un peu le from/import de Python...

In [4]:
module M = struct let x = 1 end
let _ = M.x
open M
let _ = x
Out[4]:
module M : sig val x : int end
Out[4]:
- : int = 1
Out[4]:
- : int = 1

Le risque d'utiliser open est le même que celui avec from/import en Python: on risque d'écraser des définitions existantes.

In [5]:
let s = "Charlie"
module M = struct let s = "Fred" end
open M
(* on a perdu Charlie! *)
let _  = s
Out[5]:
val s : string = "Charlie"
Out[5]:
module M : sig val s : string end
Out[5]:
- : string = "Fred"

Si l'on pouvait "refermer" le open M, on retrouverait Charlie! Comment faire?

Solution 1 la syntaxe let open M in ...

In [62]:
let hd l =
  let open LList in 
  match l with
    | Empty -> raise Empty_list
    | Cons cell -> cell.hd
Out[62]:
val hd : 'a LList.llist -> 'a = <fun>
In [68]:
Empty (* erreur: on a "refermé" MList *)

File "[68]", line 1, characters 0-5:
1 | Empty (* erreur: on a "refermé" MList *)
    ^^^^^
Error: Unbound constructor Empty

Solution 2 la syntaxe M.(...)

In [63]:
let rec somme l = match l with
  | LList.Empty -> raise LList.Empty_list
  | LList.Cons cell -> LList.(cell.hd + somme cell.tl)
Out[63]:
val somme : int LList.llist -> int = <fun>

Définitions publiques et privées¶

Revenons sur la notion de signature - ou interface, quand il s'agit de modules-fichiers.

Nous avons vu que la signature détermine ce qui est exporté par le module, ce qui est public.

Ce qui n'est pas annoncé dans la signature est à usage interne au module, donc privé.

In [64]:
module type S = sig  val x : int end
(* tout module signé par S exporte un entier x, ET RIEN D'AUTRE *)
Out[64]:
module type S = sig val x : int end
In [69]:
module M : S = struct   (* un module signé avec S *)
  let x = 1  (* public *)
  let y = 2  (* privé *)
end
Out[69]:
module M : S
In [11]:
let _ = M.x (* x est public, je peux en parler en dehors du module *)
Out[11]:
- : int = 1

Au contraire, je ne peux pas parler des définitions privées à l'extérieur du module.

Et ce n'est pas parce que j'ouvre un module que j'accède à ses définitions "privées"

In [12]:
open M 
let _ = y

File "[12]", line 2, characters 8-9:
2 | let _ = y
            ^
Error: Unbound value y

Notion de type opaque¶

La signature d'un module peut permettre d'exporter une déclaration de type sans dire à quoi ce type est égal. On parle alors de type opaque, ou de type abstrait.

In [13]:
module type MAILER = sig

   type address           (* <- type opaque *)
   type message = string  (* <- type public *)  

   val send_mail : address -> message -> unit
   
   exception IllegalMailAddress of string
   val address_of_string : string -> address
   val string_of_address : address -> string

end
Out[13]:
module type MAILER =
  sig
    type address
    type message = string
    val send_mail : address -> message -> unit
    exception IllegalMailAddress of string
    val address_of_string : string -> address
    val string_of_address : address -> string
  end

Un type opaque t s'accompagne souvent de fonctions permettant de construire des objets de type t.

Dans l'exemple précédent, c'est la fonction address_of_string qui permet de construire une adresse. Il n'y a aucun autre moyen de construire une adresse (sauf à l'intérieur du module).

Je vais maintenant définir un module qui implémente la signature MAILER.

In [14]:
module Mailer : MAILER = struct  (* <- notez le ":" *)

  type address = string  (* <- définition privée du type opaque *)
  type message = string
  
  let send_mail dst title = 
    Format.sprintf "mail -s %s %s" title dst |> Unix.system |> ignore
    
  exception IllegalMailAddress of string
  
  let address_of_string str = 
    if String.contains str '@'
    then str
    else raise (IllegalMailAddress str)
  
  let string_of_address addr = addr
  
end
Out[14]:
module Mailer : MAILER

A l'extérieur du module, j'ignore que address est un alias du type string. Je ne peux donc pas passer directement une chaîne de caractères en paramètre à sendmail. Je dois "construire" une addresse en utilisant la fonction address_of_string.

In [15]:
let () = Mailer.send_mail "titi@unice.fr" "hello!"

File "[15]", line 1, characters 26-41:
1 | let () = Mailer.send_mail "titi@unice.fr" "hello!"
                              ^^^^^^^^^^^^^^^
Error: This expression has type string but an expression was expected of type
         Mailer.address
In [16]:
let () = 
  Mailer.send_mail (Mailer.address_of_string "titi@unice.fr") "hello!"

Null message body; hope that's ok

Comme précédemment, ouvrir le module avec open ne change rien au problème: open M ne fait rentrer dans l'espace de nom que les définitions exportées par le module M, celles qui sont cachées restent cachées.

In [17]:
open Mailer
let () = Mailer.send_mail "titi@unice.fr" "hello!"

File "[17]", line 2, characters 26-41:
2 | let () = Mailer.send_mail "titi@unice.fr" "hello!"
                              ^^^^^^^^^^^^^^^
Error: This expression has type string but an expression was expected of type
         Mailer.address

Paramétricité¶

On utilise souvent les modules pour représenter des structures de données comme des listes, des arbres, des "ensembles", des piles, des files, etc.

Ces structures de données sont des "conteneurs" de données. Le type des données contenues est un paramètre ajustable.

On veut pouvoir manipuler de la même façon des listes d'entiers et des listes de flottants.

Il y a deux façons de gérer cette paramétricité:

  • utiliser un type polymorphe
    • on aura un seul module qui définit les piles
  • utiliser un foncteur, un module paramétré par un autre module
    • on aura un module "piles d'entiers",
    • un autre module "piles de flottants",
    • etc.

Pour illustrer ces deux formes de paramétricité, nous allons prendre un exemple simple: les piles.

Rappelons qu'une pile est un conteneur LIFO (last in, first out):

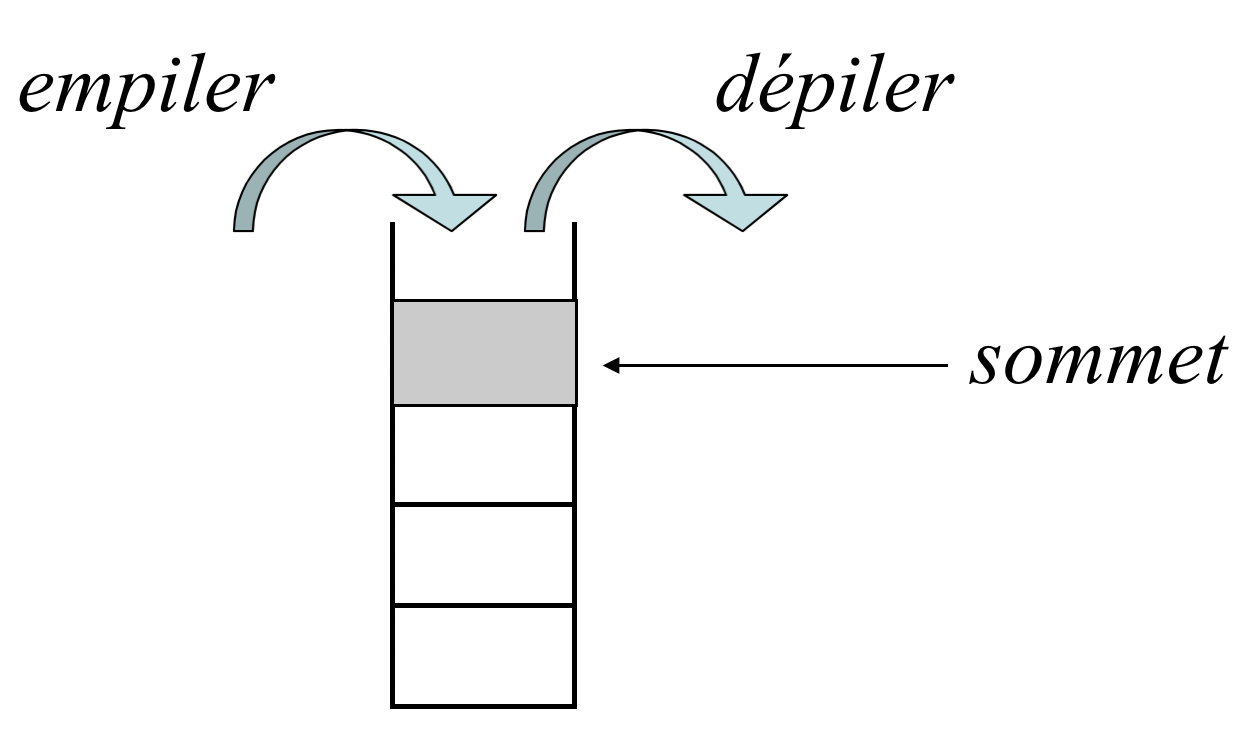
Première approche: module Pile avec type polymorphe¶

Je commence par déclarer une signature pour mon module. En plus des fonctions qui permettent de manipuler une pile, mon module devra contenir :

  • une définition du type des piles: ce sera un type opaque polymorphe
  • une exception levée lorsqu'on essaie de lire le sommet d'une pile vide
In [66]:
module type PILE = sig

  type 'a pile                     (* le type d'une pile d'objets de type 'a *)
  
  val pile_vide : 'a pile          (* la constante pile vide *)
  val empile : 'a -> 'a pile -> 'a pile

  exception Pile_vide              (* levée par depile et sommet *)
  val depile : 'a pile -> 'a pile 
  val sommet : 'a pile -> 'a

end
Out[66]:
module type PILE =
  sig
    type 'a pile
    val pile_vide : 'a pile
    val empile : 'a -> 'a pile -> 'a pile
    exception Pile_vide
    val depile : 'a pile -> 'a pile
    val sommet : 'a pile -> 'a
  end

Je dois maintenant implémenter cette signature.

Il y a plusieurs possibilités, mais la plus naturelle consiste à représenter une pile à l'aide d'une liste.

Je vais donc écrire un module qui définira le type 'a pile comme égal à 'a list.

In [19]:
module Pile = struct
   type 'a pile = 'a list  (* <- je concrétise le type opaque abstrait 'a pile *)

   let pile_vide = []
   let empile x p = x :: p
   
   exception Pile_vide
   
   let depile p = match p with
     | []      -> raise Pile_vide
     | _ :: p2 -> p2
     
   let sommet p = 
     try List.hd p 
     with Failure _ -> raise Pile_vide
end
Out[19]:
module Pile :
  sig
    type 'a pile = 'a list
    val pile_vide : 'a list
    val empile : 'a -> 'a list -> 'a list
    exception Pile_vide
    val depile : 'a list -> 'a list
    val sommet : 'a list -> 'a
  end

Extension de module avec include¶

Je voudrais maintenant rajouter des fonctions to_string, sort, et sum à mon module pour pouvoir afficher, trier, ou sommer une pile.

Le type polymorphe 'a pile me pose un problème: en effet, je ne sais pas à l'avance comment je dois afficher un objet de type 'a, ni comment je dois comparer ou sommer deux objets de type 'a.

La solution, déjà vue avec les listes, consiste à rajouter des paramètres aux fonctions to_string, sort, et sum pour fixer comment je dois gérer mes objets de type 'a.

Plus précisément, si j'ai une pile pile1 de type int pile, à l'aide de mon module Pile, je pourrai

  • l'afficher en utilisant Pile.to_string string_of_int pile1
  • la trier en ordre croissant en utilisant Pile.sort compare pile1
  • calculer sa somme en utilisant Pile.sum (+) 0 pile1

Je vais définir une nouvelle signature PILE2 pour mon module de piles imprimables, triables, et sommables.

Pour éviter de recopier le début de la signature PILE, je vais utiliser le mot-clé include.

In [67]:
module type PILE2 = sig
   include PILE (* copier-collé du contenu de la signature PILE *)
   
   val to_string : ('a -> string) -> 'a pile -> string
   val sort : ('a -> 'a -> int) -> 'a pile -> 'a pile
   val sum : ('a -> 'a -> 'a) -> 'a -> 'a pile -> 'a
end
Out[67]:
module type PILE2 =
  sig
    type 'a pile
    val pile_vide : 'a pile
    val empile : 'a -> 'a pile -> 'a pile
    exception Pile_vide
    val depile : 'a pile -> 'a pile
    val sommet : 'a pile -> 'a
    val to_string : ('a -> string) -> 'a pile -> string
    val sort : ('a -> 'a -> int) -> 'a pile -> 'a pile
    val sum : ('a -> 'a -> 'a) -> 'a -> 'a pile -> 'a
  end

Attention à ne pas confondre open et include

  • open change l'espace de noms, mais il n'introduit pas de déclarations
  • include ajoute des déclarations; c'est une sorte de "copier-collé"

De la même façon, je vais définir un module Pile2 qui implémente la signature PILE2.

In [21]:
module Pile2  = struct
   include Pile
   
   let to_string f pile = (String.concat "|" (List.map f pile)) ^ "]"
   let sort cmp pile = List.sort cmp pile
   let sum plus zero pile = List.fold_left plus zero pile
end
Out[21]:
module Pile2 :
  sig
    type 'a pile = 'a list
    val pile_vide : 'a list
    val empile : 'a -> 'a list -> 'a list
    exception Pile_vide
    val depile : 'a list -> 'a list
    val sommet : 'a list -> 'a
    val to_string : ('a -> string) -> 'a list -> string
    val sort : ('a -> 'a -> int) -> 'a list -> 'a list
    val sum : ('a -> 'b -> 'a) -> 'a -> 'b list -> 'a
  end
In [22]:
let p = Pile2.(pile_vide |> empile 1 |> empile 2 |> empile 3) in
Pile2.to_string string_of_int p
Out[22]:
- : string = "3|2|1]"

Deuxième approche: le module Pile avec foncteur¶

Dans l'exemple précédent, on avait besoin d'avoir quelques opérations élémentaires sur les objets de type 'a que l'on allait mettre dans les piles.

Dans cette deuxième approche, je vais commencer par regrouper toutes les opérations élémentaires dont j'ai besoin dans une signature.

In [23]:
module type EMPILABLE = sig
  type  t   (* <- le type 'a de tout à l'heure, maintenant opaque *)

  (* les opérations élémentaires sur des objets empilables *)
  val to_string : t -> string  (* afficher *)
  val compare : t -> t -> int  (* comparer *)
  val add : t -> t -> t        (* ajouter  *)
  val null : t                 (* neutre de l'addition *)
end
Out[23]:
module type EMPILABLE =
  sig
    type t
    val to_string : t -> string
    val compare : t -> t -> int
    val add : t -> t -> t
    val null : t
  end

Ceci fait, je peux maintenant définir un foncteur Pile qui prend en paramètre un module E d'objets empilables.

Je vais utiliser la syntaxe module Pile (E:EMPILABLE) = ....

Ce foncteur Pile n'est pas encore un module: il faudra que je fixe le module E pour obtenir un module. C'est une sorte de "moule" pour fabriquer des modules "pile de ...".

Par exemple, une fois que j'aurai défini un module EntierEmpilable, je pourrai fabriquer un module Pile_Entiers en utilisant mon foncteur et en instanciant E avec EntierEmpilable.

À l'intérieur du module Pile, pour afficher un objet empilable, j'utiliserai E.to_string. Ma fonction Pile.to_string n'aura donc plus besoin du paramètre de type 'a -> string de tout à l'heure, c'est le choix du module E qui fixera la fonction d'affichage des objets empilés.

Assez parlé, voyons ce que cela donne...

In [24]:
module Pile3 (E : EMPILABLE) = struct
   type pile = E.t list  (* <- le type des piles n'est plus un type polymorphe *)
   
   let empile x p = x :: p   let depile = List.tl   let sommet = List.hd
   
   let to_string pile = (String.concat "|" (List.map E.to_string pile)) ^ "]"
   let sum pile = List.fold_left E.add E.null pile
   let sort pile = List.sort E.compare pile
end
Out[24]:
module Pile3 :
  functor (E : EMPILABLE) ->
    sig
      type pile = E.t list
      val empile : 'a -> 'a list -> 'a list
      val depile : 'a list -> 'a list
      val sommet : 'a list -> 'a
      val to_string : E.t list -> string
      val sum : E.t list -> E.t
      val sort : E.t list -> E.t list
    end
In [25]:
module EntierEmpilable : EMPILABLE = struct
   type t = int   (* <- le type opaque de EMPILABLE doit être "instancié" *)
   let to_string = string_of_int
   let compare = compare
   let add = (+)
   let null = 0
end

module Pile_Entiers = Pile3(EntierEmpilable)
Out[25]:
module EntierEmpilable : EMPILABLE
Out[25]:
module Pile_Entiers :
  sig
    type pile = EntierEmpilable.t list
    val empile : 'a -> 'a list -> 'a list
    val depile : 'a list -> 'a list
    val sommet : 'a list -> 'a
    val to_string : EntierEmpilable.t list -> string
    val sum : EntierEmpilable.t list -> EntierEmpilable.t
    val sort : EntierEmpilable.t list -> EntierEmpilable.t list
  end

Le foncteur Set.Make de la librairie standard¶

Vous aurez peut-être l'occasion d'écrire des foncteurs, mais vous aurez aussi, et surtout, l'occasion d'avoir à les utiliser.

La librairie standard comporte un certain nombre de foncteurs; en particulier, si vous voulez une structure de données efficace pour représenter un "ensemble de ...", vous pourrez utiliser le module Set, mais il vous faudra en passer par un foncteur...

En effet, de même qu'en Python un ensemble ne pouvait contenir que des données "hashables", les modules ensembles d'OCaml ne peuvent accueillir que des objets "ordonnables".

Pour créer un module "ensemble de truc", je vais donc devoir créer un module Truc puis générer un module EnsembleTruc en appelant le foncteur Set.Make. Au final, vous écrirez quelque chose comme

module EnsembleTruc = Set.Make(Truc)
let paire truc1 truc2 = 
   EnsembleTruc.(union (singleton truc1) (singleton truc2))

Si on consulte le manuel de référence, on voit en effet que le module Set contient les déclarations suivantes

module Set = struct
   module type S = sig ... end            
   (* la signature d'un module "ensemble de trucs" *)

   module type OrderedType = sig ... end  
   (* la signature d'un module "ordonnable" *)

   module Make (Elt:OrderedType) : S = struct ... end
   (* le foncteur OrderedType -> S *) 
end

Ainsi, mon module Truc devra avoir la signature Set.OrderedType

Toujours dans le manuel de référence, on trouve la définition de la signature Set.OrderedType

module type OrderedType = sig
  type t                      (* the type of set elements *)
  val compare : t -> t -> int (* a total ordering function over the set elements *)
end

Supposons que je veuille faire des ensembles de couples d'entiers qui représentent des fractions.

Pour comparer le couple (a,b) et le couple (c,d), je vais donc regarder le signe de $ad - bc$.

In [26]:
module CoupleEntiers = struct
  type t = int * int
  let compare (a,b) (c,d) = a * d - b * c
end

module EnsembleFractions = Set.Make(CoupleEntiers)
Out[26]:
module CoupleEntiers :
  sig type t = int * int val compare : int * int -> int * int -> int end
Out[26]:
module EnsembleFractions :
  sig
    type elt = CoupleEntiers.t
    type t = Set.Make(CoupleEntiers).t
    val empty : t
    val is_empty : t -> bool
    val mem : elt -> t -> bool
    val add : elt -> t -> t
    val singleton : elt -> t
    val remove : elt -> t -> t
    val union : t -> t -> t
    val inter : t -> t -> t
    val disjoint : t -> t -> bool
    val diff : t -> t -> t
    val compare : t -> t -> int
    val equal : t -> t -> bool
    val subset : t -> t -> bool
    val iter : (elt -> unit) -> t -> unit
    val map : (elt -> elt) -> t -> t
    val fold : (elt -> 'a -> 'a) -> t -> 'a -> 'a
    val for_all : (elt -> bool) -> t -> bool
    val exists : (elt -> bool) -> t -> bool
    val filter : (elt -> bool) -> t -> t
    val partition : (elt -> bool) -> t -> t * t
    val cardinal : t -> int
    val elements : t -> elt list
    val min_elt : t -> elt
    val min_elt_opt : t -> elt option
    val max_elt : t -> elt
    val max_elt_opt : t -> elt option
    val choose : t -> elt
    val choose_opt : t -> elt option
    val split : elt -> t -> t * bool * t
    val find : elt -> t -> elt
    val find_opt : elt -> t -> elt option
    val find_first : (elt -> bool) -> t -> elt
    val find_first_opt : (elt -> bool) -> t -> elt option
    val find_last : (elt -> bool) -> t -> elt
    val find_last_opt : (elt -> bool) -> t -> elt option
    val of_list : elt list -> t
    val to_seq_from : elt -> t -> elt Seq.t
    val to_seq : t -> elt Seq.t
    val add_seq : elt Seq.t -> t -> t
    val of_seq : elt Seq.t -> t
  end
In [27]:
let s = EnsembleFractions.of_list [(1,2); (3,4); (6,8)]

let l = EnsembleFractions.elements s
Out[27]:
val s : EnsembleFractions.t = <abstr>
Out[27]:
val l : EnsembleFractions.elt list = [(1, 2); (3, 4)]

C'est assez lourd pour manipuler des ensembles, certes...

Astuce

Je peux économiser du code. Par exemple, je peux fabriquer le module IntSet des ensembles d'entiers en une seule ligne, en n'introduisant pas un module Int qui serait d'usage très limité.

In [28]:
module IntSet = Set.Make(struct type t = int let compare = compare end)
Out[28]:
module IntSet :
  sig
    type elt = int
    type t
    val empty : t
    val is_empty : t -> bool
    val mem : elt -> t -> bool
    val add : elt -> t -> t
    val singleton : elt -> t
    val remove : elt -> t -> t
    val union : t -> t -> t
    val inter : t -> t -> t
    val disjoint : t -> t -> bool
    val diff : t -> t -> t
    val compare : t -> t -> int
    val equal : t -> t -> bool
    val subset : t -> t -> bool
    val iter : (elt -> unit) -> t -> unit
    val map : (elt -> elt) -> t -> t
    val fold : (elt -> 'a -> 'a) -> t -> 'a -> 'a
    val for_all : (elt -> bool) -> t -> bool
    val exists : (elt -> bool) -> t -> bool
    val filter : (elt -> bool) -> t -> t
    val partition : (elt -> bool) -> t -> t * t
    val cardinal : t -> int
    val elements : t -> elt list
    val min_elt : t -> elt
    val min_elt_opt : t -> elt option
    val max_elt : t -> elt
    val max_elt_opt : t -> elt option
    val choose : t -> elt
    val choose_opt : t -> elt option
    val split : elt -> t -> t * bool * t
    val find : elt -> t -> elt
    val find_opt : elt -> t -> elt option
    val find_first : (elt -> bool) -> t -> elt
    val find_first_opt : (elt -> bool) -> t -> elt option
    val find_last : (elt -> bool) -> t -> elt
    val find_last_opt : (elt -> bool) -> t -> elt option
    val of_list : elt list -> t
    val to_seq_from : elt -> t -> elt Seq.t
    val to_seq : t -> elt Seq.t
    val add_seq : elt Seq.t -> t -> t
    val of_seq : elt Seq.t -> t
  end

Comment savoir quelles opérations existent sur les ensembles?

Il suffit d'aller voir la documentation de la signature Set.S dans le manuel de référence.

Faisons le point¶

Nous avons vu deux façons de déclarer un module Pile "paramétré" par le type des éléments qui seront empilés

  • utiliser un type polymorphe 'a pile
  • utiliser un foncteur et un type générique opaque t à la place de la variable de type 'a.

Dans les deux cas, le but recherché est le polymorphisme paramétrique.

OCaml s'assure que le typage paramétrique ne casse pas les règles de typage. Certaines situations nécessitent un peu plus de travail que ce que nous avons vu pour arriver à satisfaire les contraintes de type, et requièrent l'emploi du mot-clé with, que nous verrons plus loin.

Notion de persistance¶

Nous avons fait un module Pile qui manipule des piles sans les modifier: quand on empile un élément sur une pile p, on obtient une pile p' qui contient le résultat de l'opération, mais la pile p reste inchangée.

empile : 'a -> 'a pile -> 'a pile

On parle de structure de données "fonctionnelle" ou plus justement de structure de données persistante.

Une autre approche consiste à modifier la pile passée en paramètre plutôt que de renvoyer une nouvelle pile.

empile : 'a -> 'a pile -> unit

On parle alors de structure de donnée "mutable", ou "impérative", ou plus justement de structure de données non persistante.

Chaque approche a ses avantages, mais un programmeur rigoureux évitera de mélanger les deux en général.

Remarque: persistant ne veut pas forcément dire immutable; certaines structures de données persistantes "font comme si" elles étaient immutables, mais utilisent en interne des mutations (voir le livre programmer avec Ocaml pour de nombreux exemples).

Piles non persistantes (ou "impératives")¶

Nous allons maintenant écrire un module qui implémente des piles non persistantes. Commençons par fixer la signature.

In [ ]:
module type PILE_IMP =
   type 'a pile

Avancé: le mot-clé with¶

Le mot-clé with permet de créer une nouvelle signature en instanciant un type opaque dans une signature.

In [44]:
module type T = sig 
   type t (* <- opaque *)
   val null : t 
end
Out[44]:
module type T = sig type t val null : t end
In [45]:
module type INT = T with type t = int   (* <- j'instancie t avec int *)
Out[45]:
module type INT = sig type t = int val null : t end
In [46]:
module Int : INT = struct 
   type t = int  
   let null = 0
end
Out[46]:
module Int : INT
In [47]:
Int.null
Out[47]:
- : Int.t = 0

Si j'avais signé Int avec T, Int.null s'afficherait comme <abstr>.

Bourbaki rencontre OCaml¶

Nous allons maintenant définir quelques structures algébriques que certains ont dû rencontrer dans leurs cours de math:

  • les monoïdes : ce sont des ensembles sur lequel on peut faire des sommes, non nécessairement commutatives
  • les anneaux : on rajoute la notion de produit

Avertissement Le but premier est d'illustrer l'utilisation des modules, des foncteurs et quelques usages du mot-clé with. Nous nous inspirons des structures algébriques que vous verriez en mathématiques, mais les axiomes que satisfont ces structures algébriques ne vont pas être modélisés dans OCaml... il nous faudrait un langage plus riche. On verra à la fin comment tester ces axiomes de manière automatique pour les structures algébriques finies.

Commençons par les monoides: un monoïde définit une loi de composition interne qui admet un élément neutre.

In [48]:
module type MONOIDE = sig
  type t                    (* le type des éléments du monoide *)
  val compose : t -> t -> t (* la loi de composition interne   *)
  val neutre : t            (* l'élément neutre *)
end
Out[48]:
module type MONOIDE = sig type t val compose : t -> t -> t val neutre : t end

Définissons quelques monoides pour illustrer cette notion.

In [49]:
module N_Add = struct  (* les entiers avec l'addition et le neutre 0 *)
   type t = int
   let compose n m = n + m
   let neutre = 0
end
Out[49]:
module N_Add :
  sig type t = int val compose : int -> int -> int val neutre : int end
In [50]:
module N_Mult = struct  (* les entiers non nuls avec la multiplication et le neutre 1 *)
   type t = int
   let compose n m = n * m
   let neutre = 1
end
Out[50]:
module N_Mult :
  sig type t = int val compose : int -> int -> int val neutre : int end
In [51]:
module Mots = struct  (* les mots avec la concaténation et le mot vide *)
   type t = string
   let compose s1 s2 = s1 ^ s2
   let neutre = ""
end
Out[51]:
module Mots :
  sig
    type t = string
    val compose : string -> string -> string
    val neutre : string
  end
In [52]:
module Bool_Xor = struct  (* les booléens avec le "ou exclusif" *)
   type t = bool
   let compose b1 b2 = b1 <> b2
   let neutre = false
end
Out[52]:
module Bool_Xor :
  sig type t = bool val compose : 'a -> 'a -> bool val neutre : bool end
In [53]:
module Bool_And = struct  (* les booléens avec le "et" *)
   type t = bool
   let compose b1 b2 = b1 && b2
   let neutre = true
end
Out[53]:
module Bool_And :
  sig type t = bool val compose : bool -> bool -> bool val neutre : bool end

Passons maintenant aux anneaux.

Un anneau est la donnée de deux lois de composition interne sur le même ensemble, chacune définissant un monoïde.

In [54]:
module type ANNEAU = sig
   type t
   val add : t -> t -> t
   val mult : t -> t -> t
   val zero : t
   val un : t
end
Out[54]:
module type ANNEAU =
  sig
    type t
    val add : t -> t -> t
    val mult : t -> t -> t
    val zero : t
    val un : t
  end

Traduisons l'idée qu'un anneau est constitué de deux monoides par un foncteur. Toute la difficulté est d'exprimer que les monoides portent "sur un même ensemble".

In [55]:
module Make_Anneau (Add: MONOIDE) (Mult: MONOIDE with type t = Add.t) 
   : ANNEAU with type t = Add.t
   = struct
   type t = Add.t
   let add = Add.compose
   let mult = Mult.compose
   let zero = Add.neutre
   let un = Mult.neutre
end
Out[55]:
module Make_Anneau :
  functor
    (Add : MONOIDE) (Mult : sig
                              type t = Add.t
                              val compose : t -> t -> t
                              val neutre : t
                            end) ->
    sig
      type t = Add.t
      val add : t -> t -> t
      val mult : t -> t -> t
      val zero : t
      val un : t
    end
In [56]:
module N = Make_Anneau(N_Add)(N_Mult)
Out[56]:
module N :
  sig
    type t = N_Add.t
    val add : t -> t -> t
    val mult : t -> t -> t
    val zero : t
    val un : t
  end
In [57]:
module Bool = Make_Anneau(Bool_Xor)(Bool_And)
Out[57]:
module Bool :
  sig
    type t = Bool_Xor.t
    val add : t -> t -> t
    val mult : t -> t -> t
    val zero : t
    val un : t
  end
In [58]:
module MalForme = Make_Anneau(N_Add)(Mots)

File "[58]", line 1, characters 37-41:
1 | module MalForme = Make_Anneau(N_Add)(Mots)
                                         ^^^^
Error: Signature mismatch:
       ...
       Type declarations do not match:
         type t = string
       is not included in
         type t = N_Add.t
       File "[55]", line 1, characters 54-68: Expected declaration
       File "[51]", line 2, characters 3-18: Actual declaration

On pourrait continuer ainsi et définir l'anneau des polynomes, l'anneau des matrices, etc. Vous le ferez peut-être en TP?

Pour conclure, nous allons simplement indiquer comment on peut formaliser les axiomes d'un monoïde et les tester à l'aide d'un foncteur de test.

Rappelons ces axiomes

  • l'axiome d'associativité $$\forall x,y,z\in M. (xy)z~=~x(yz)$$

  • l'axiome de l'élément neutre $$\forall x\in M. xe = ex = x$$

Pour pouvoir écrire nos axiomes, nous avons donc besoin de quantifier sur les éléments de l'ensemble.

In [59]:
module type MONOIDE_TESTABLE = sig
   include MONOIDE
   val forall : (t -> bool) -> bool
end

module Test_Monoide(M : MONOIDE_TESTABLE) = struct

   let ( * ) = M.compose
   
   let () = (* test de l'axiome d'associativité *)
      assert (M.forall (fun x -> (M.forall (fun y -> M.forall (fun z ->
         (x*y)*z = x*(y*z)
      )))))
      
   let e = M.neutre
   
   let () = (* test de l'axiome du neutre *)
      assert (M.forall (fun x -> 
         x*e=x && e*x=x
      ))
end
Out[59]:
module type MONOIDE_TESTABLE =
  sig
    type t
    val compose : t -> t -> t
    val neutre : t
    val forall : (t -> bool) -> bool
  end
Out[59]:
module Test_Monoide :
  functor (M : MONOIDE_TESTABLE) ->
    sig val ( * ) : M.t -> M.t -> M.t val e : M.t end
In [60]:
module Bool_Xor_Testable = struct
   include Bool_Xor
   let forall enonce = (enonce false) && (enonce true) 
end
Out[60]:
module Bool_Xor_Testable :
  sig
    type t = bool
    val compose : 'a -> 'a -> bool
    val neutre : bool
    val forall : (bool -> bool) -> bool
  end
In [61]:
module Test_Bool = Test_Monoide(Bool_Xor_Testable)

(* pas d'erreur: le xor est bien associatif et admet bien l'élément neutre false *)
Out[61]:
module Test_Bool :
  sig
    val ( * ) :
      Bool_Xor_Testable.t -> Bool_Xor_Testable.t -> Bool_Xor_Testable.t
    val e : Bool_Xor_Testable.t
  end

Exercice d'algèbre assistée par ordinateur (requis: la notion de groupe)

  1. le monoide des booléens avec la loi de composition interne "ou exclusif" est-il un groupe?
  2. le monoide des booléens avec la loi de composition interne "et logique" est-il un groupe?
  3. définissez une signature pour les groupes, et un testeur d'axiomes des groupes, et vérifiez vos réponses.