Programmation fonctionnelle¶

TD 3 : Programmer avec des arbres¶

Etienne Lozes, Julien Provillard - 2021¶

Exercice 1 : Complexes¶

On se donne deux représentations différentes des complexes:

l'une sous leur forme cartésienne via le type cartesien
l'autre sous leur forme polaire via le type polaire

type cartesien = {re: float; im: float}
type polaire = {modulus: float; arg: float}

Définissez une fonction polaire_to_cartesien qui convertit un complexe sous forme polaire vers sa représentation cartésienne.
Définissez une fonction cartesien_to_polaire qui convertit un complexe sous forme cartésienne vers sa représentation polaire. On rappelle l'existence de la fonction atan2 telle que atan2 y x renvoie une mesure de l'angle entre le vecteur directeur de l'axe des abscisses et le vecteur de coordonnées (x, y).
On cherche maintenant à manipuler les complexes sans distinction sur leur représentation. Définissez un type complexe qui permet de travailler simultanément sur les deux représentations possibles.
Définissez une fonction conj qui renvoie le conjugué d'un complexe. Le type de la fonction doit donc être complexe -> complexe.
Définissez une fonction add: complexe -> complexe -> complexe qui calcule la somme de deux nombres complexes.
Définissez une fonction mul: complexe -> complexe -> complexe qui calcule le produit de deux nombres complexes.

Exercice 2 : Tas d'appariement¶

Un tas, aussi appellé file de priorité est une structure de données qui dispose des opérations suivantes:

get_min : renvoie le plus petit élément du tas
remove_min : enlève le plus petit élément du tas
insert x : ajoute l'élément x au tas

Un tas d'appariement (en anglais pairing heap) est un tas qui admet facilement une implémentation "purement fonctionnelle" (on dira plutôt persistante, au sens où on ne modifie pas de manière visible la structure de données, on en obtient toujours une copie avec la mise à jour effectuée). On supposera dans la suite pour simplifier que les éléments d'un tas sont des entiers (on verra plus tard comment on pourrait généraliser de manière propre à un ensemble ordonné quelconque).

Un arbre d'appariement est un arbre d'arité quelconque contenant les entiers du tas sur ses nœuds et vérifiant de plus les invariants suivants:
- la racine est le plus petit élément du tas
- tous les fils immédiats de la racine sont eux-même des arbres d'appariement. Définissez un type pairing_tree permettant de représenter un arbre d'appariement.
Un tas d'appariement est soit vide, soit un arbre d'appariement. Définissez le type pairing_heap.
Définissez la fonction get_min.
On fusionne deux tas de la façon suivante:
- si l'un des tas est vide, le résultat de leur fusion est l'autre tas
- si les deux tas sont non vides, celui avec la racine la plus grande devient un sous-tas de la racine la plus petite (cf figure). Définissez la fonction merge2 : pairing_heap -> pairing_heap -> pairing_heap qui fusionne deux tas.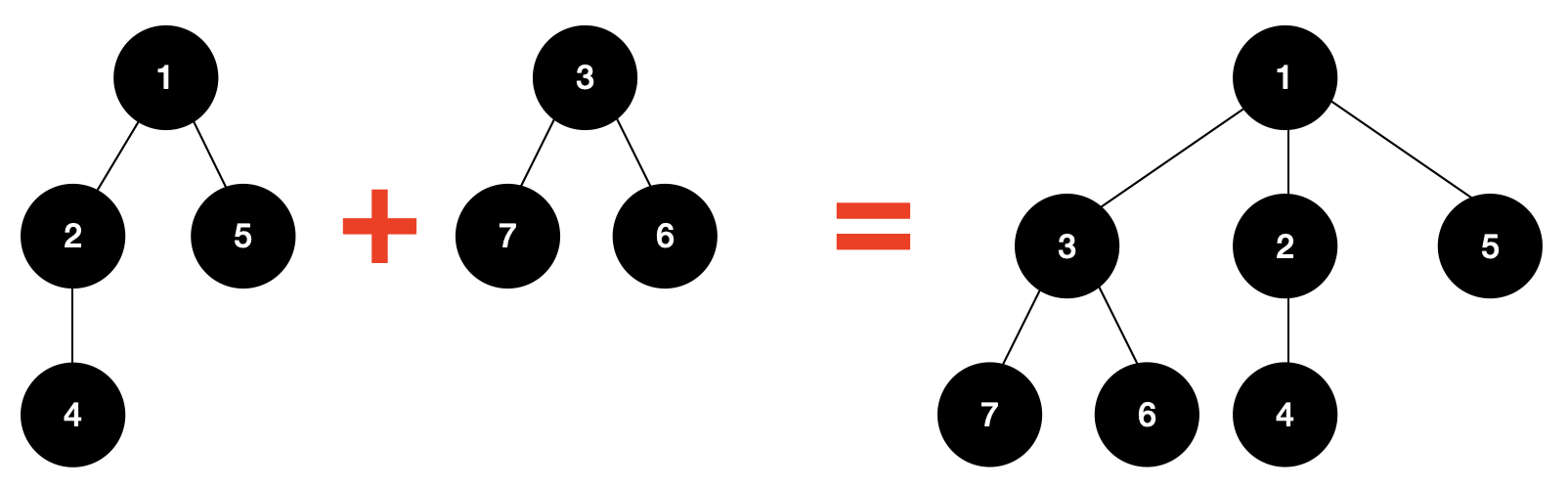
Définissez la fonction insert: int -> pairing_heap -> pairing_heap. Pour cela on crée un nouveau tas avec l'élément à insérer et on le fusionne avec le tas passé en paramètre.
La fonction remove_min: pairing_tree -> pairing_heap n'est définie que sur un tas non vide (donc un arbre). Il suffit de fusionner tous les fils de la racine. On doit donc définir une fonction auxiliaire merge: pairing_tree list -> pairing_heap qui fusionne un nombre arbitraire d'arbres. On procède par récurrence sur le nombre d'arbres en utilisant la fonction merge2 définie précédemment:
- s'il y a zéro ou un arbre, on sait faire
- s'il y a deux premiers arbres t1 et t2 et encore une liste tl d'autres arbres, on fusionne d'une part t1 et t2, d'autre part on fusionne tl par récurrence, puis on fusionne ces deux tas fusionnés.
Définir une fonction from_list qui crée un tas d'appariement à partir d'une liste
Définir une fonction to_list qui crée la liste (ordonnée) des éléments d'un tas d'appariement
En déduire une fonction heap_sort qui trie une liste par l'algorithme du tri par tas.

Exercice 3 : Polynômes creux¶

On représente un monôme par son coefficient (non nul) et son degré. Un polynôme "creux" (avec beaucoup de coefficients à zéro) est représenté succinctement par la liste de ses monômes non nuls triée par degrés décroissants.

type monome = {coeff: float; deg: int}
type polynome = monome list

Remarquez que le type polynome est un alias du type monome list. On verra plus tard comment abstraire et rendre opaque un type tel que polynome pour mieux mettre en avant le fait qu'un polynôme est une liste de monômes qui vérifie certains invariants, et non une liste quelconque de monômes. Mais comme c'était déjà le cas dans l'exercice précédent, toutes les opérations que nous allons définir sur ce type concret devront préserver ces invariants.

Comment est représenté le polynôme nul?
Définissez une fonction degree qui renvoie le degré d'un polynôme.
Quel est le type de la fonction degree? Pouvons-nous y faire quelque chose?
Définissez l'opérateur ++ qui réalise la somme de deux polynômes.
Définissez l'opérateur ~~ qui renvoie l'opposé d'un polynôme. En déduire l'opérateur -- qui réalise la différence de deux polynômes.
Définissez la fonction mult_monome qui réalise le produit d'un monôme et d'un polynôme. En déduire l'opérateur ** qui réalise le produit de deux polynômes.
Définissez l'opérateur // qui réalise la division euclidienne de deux polynômes.
Définissez une fonction monomes_to_polynome qui prend en argument une liste de monômes sans aucune contrainte et qui renvoie le polynôme qui correspond à leur somme.