Pour démontrer que le résultat de l’algorithme abstrait ne dépend pas de la stratégie de pioche, il nous faut tout d’abord formaliser un peu le problème.
On notera \(C\stackrel{X}{\longrightarrow} C'\) si on passe la configuration C à la configuration \(C'\) en laissant l’homme \(X\) faire une proposition; cela signifie que dans la configuration \(C\) l’homme \(X\) se trouve dans la pioche, et que soit il s’y retrouve dans \(C'\) après avoir été éconduit, soit il s’est fiancé et éventuellement un autre homme \(X'\) a été éconduit et se trouve désormais dans la pioche. Notons \(C\longrightarrow^* C'\) si on passe de C à C’ en faisant \(n\geq 0\) propositions d’hommes successives. Notons enfin \(C_0\) la configuration initiale (tout le monde est célibataire, la pioche contient tous les hommes).
Un résultat de l’algorithme est une configuration \(C\) telle que \(C_0\longrightarrow^* C\) et \(C\not\rightarrow\) (la pioche est vide dans \(C\)). On parle de système de réécriture pour la relation \(\longrightarrow\) et de forme normale pour un résultat. La propriété qu’on veut démontrer est donc l’unicité de la forme normale (et il faudrait aussi montrer son existence, mais cela vient du fait que le système de réécriture termine: il n’y a pas de chemin infini, la relation \(\longrightarrow\) est bien fondée, à vous de réfléchir comment vous prouveriez cela, ce n’est pas très compliqué).
On va généraliser le problème et supposer que l’algorithme débute dans une configuration quelconque (pas nécessairement \(C_0\)). Au passage, c’est une idée utilisée par Knuth dans ces notes de cours pour montrer comment calculer d’autres mariages stables que le mariage stable le plus favorable aux hommes, mais peu importe.
La propriété qu’on veut démontrer, pour résumer, est ce qu’on appelle la confluence du système de réécriture:
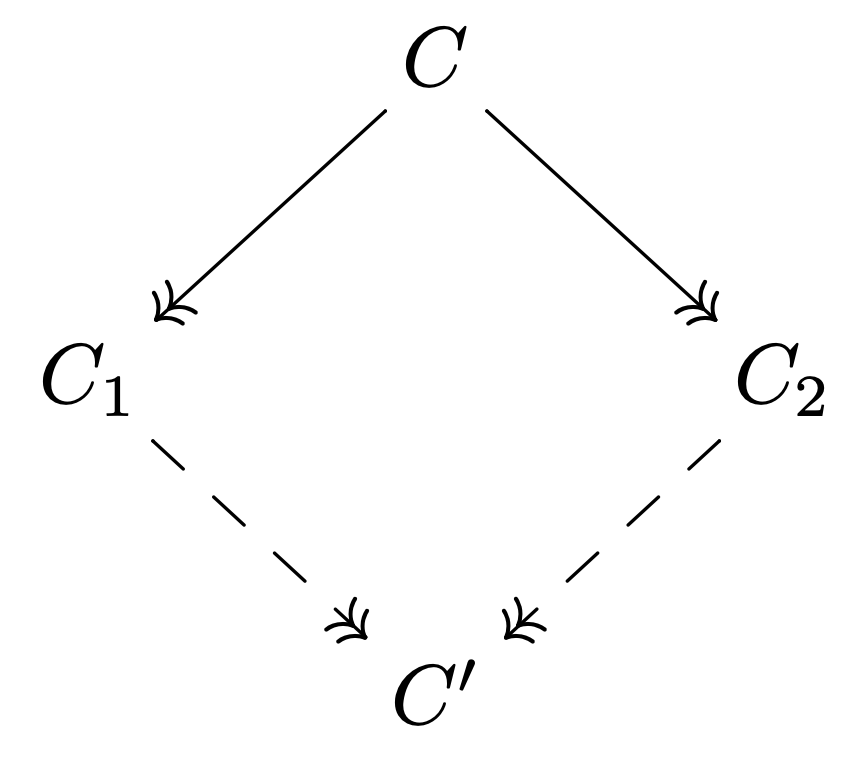
si \(C\longrightarrow^* C_1\) et \(C\longrightarrow^* C_2\), alors il existe \(C'\) telle que \(C_1\longrightarrow^* C'\) et \(C_2\longrightarrow^* C'\)

Pour la démontrer, on va montrer une propriété plus forte, appelée tout simplement la confluence forte:
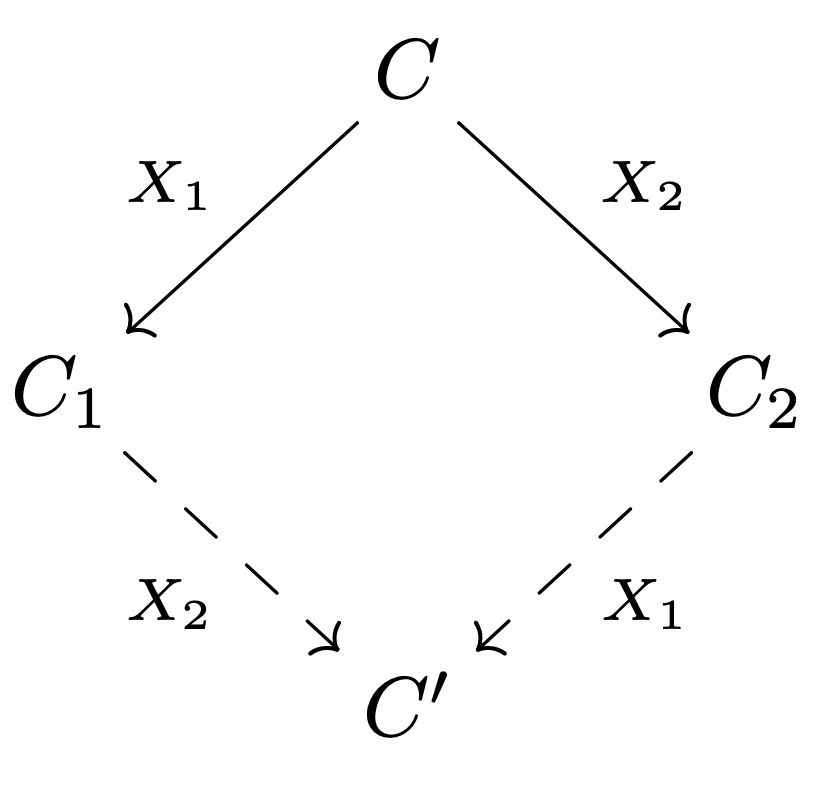
si \(C\stackrel{X_1}{\longrightarrow} C_1\) et \(C\stackrel{X_2}{\longrightarrow} C_2\), alors il existe \(C'\) telle que \(C_1\stackrel{X_2}{\longrightarrow} C'\) et \(C_2\stackrel{X_1}{\longrightarrow} C'\).
Il est facile de se convaincre (et de faire une preuve par récurrence) du fait que la confluence forte implique la confluence. Si vous voulez en savoir plus sur la réécriture et son lien avec le lambda-calcul (la théorie qui fonde la programmation fonctionnelle), je vous invite à lire ou à regarder la première séance du cours de Jean Goubault-Larrecq à l’ENS Paris-Saclay. Il est question de la confluence forte à 1h47, si vous n’avez pas le courage de tout écouter.
Pour conclure la preuve, montrons donc la confluence forte. On fixe \(C\), \(C_1\), \(C_2\), \(X_1\), \(X_2\) tels que \(C\stackrel{X_1}{\longrightarrow} C_1\) et \(C\stackrel{X_2}{\longrightarrow} C_2\), et on doit construire \(C'\) qui permet de “joindre” \(C_1\) et \(C_2\).
si \(X_1\) et \(X_2\) font leur proposition à deux femmes \(x_1\) et \(x_2\) distinctes, il est facile de voir que les données modifiées sont disjointes, on peut faire les deux opérations “en parallèle”. \(C'\) est la configuration dans laquelle \(x_1\) a le même fiancé que dans \(C_1\) et \(x_2\) a le même fiancé que dans \(C_2\).
si \(X_1\) et \(X_2\) font leur proposition à la même femme \(x\), on définit \(C'\) comme la configuration où \(x\) est fiancée à son préféré entre \(X_1\), \(X_2\) et son éventuel fiancé dans \(C\). Il est facile de voir que \(C'\) convient pour faire commuter le diagramme.