Qu'est-ce qu'un interpréteur?¶
Un interpréteur est un programme capable de lire du code écrit dans un langage et de l'exécuter. On peut aussi parler parfois (rarement) d'un évaluateur.
Exemples:
- un toplevel: évalue des expressions, exécute des commandes...
- un navigateur web: interprète du Javascript, du Webassembly, ...
- la machine virtuelle JAVA (JVM): interprète du bytecode Java
- un simulateur de micro-processeur: interprète de l'assembleur
Contrairement à un compilateur, on ne traduit pas le code dans un autre langage pour le faire exécuter par quelqu'un d'autre (le plus souvent le micro-processeur), mais on l'exécute directement.
Il est souvent plus facile d'écrire un interpréteur qu'un compilateur (exception: si on compile vers un langage très proche...).
Aperçu de l'interpréteur µRust¶
shell$ cargo run
µRust # let mut x = (3 + 4) * 5
x : isize = 35
µRust # x = x + 1
- : unit = ()
µRust # x
- : isize = 36
µRust # ^D
shell$
Mon premier interpréteur: la calculatrice¶
Nous allons commencer par écrire un petit toplevel capable d'évaluer des expressions arithmétiques simples, comme $(3+4)\times 5$.
Une expression est représentée par un arbre de syntaxe abstraite (AST).
Par exemple l'AST de l'expression $(3+4)\times 5$ est l'arbre
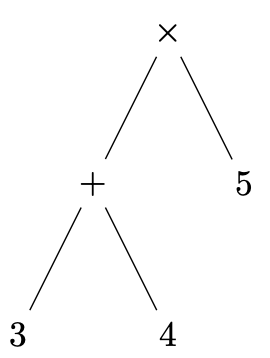
Pour représenter de tels arbres, nous allons utiliser des types de données algébriques (algebraic data type, ADT), comme vous l'avez déjà fait en OCaml
(* définition d'un arbre syntaxique en Caml *)
type expression =
| Const of int
| BinOp of expression * binop * expression
(* ... *)
type binop = PLUS | MINUS | MULT | DIV
Sauf qu'on va le faire en Rust.
pub enum Expression {
Const(isize),
BinOp(Box<Expression>, Binop, Box<Expression>),
// ...
}
pub enum Binop { Plus, Minus, Mult, Div }
Rappelons qu'en Rust, si on veut définir un type récursif, on est obligé d'expliciter les pointeurs (comme en C).
Si on avait écrit BinOp(Expression, Binop, Expression) on aurait eu un message d'erreur, car Rust n'aurait pas pu calculer
la taille mémoire nécessaire pour stocker un objet de type Expression.
En Caml ces pointeurs sont implicites...
On va ensuite écrire la fonction qui évalue l'expression arithmétique. On procède par récurrence, en faisant une définition par cas avec du pattern-matching. En Caml cela donne par exemple
let rec eval e = match e with
| Const n -> n
| BinOp(eg, Plus, ed) -> (eval eg) + (eval ed)
| BinOp(eg, Mult, ed) -> (eval eg) * (eval ed)
(* ... *)
Rappelons qu'en Rust, le branchement par motif (pattern-matching) existe aussi!
// version simplifiée
impl Expression {
fn eval(&self) -> isize {
match self {
Const(n) => n,
BinOp(eg, Plus, ed) => eg.eval() + ed.eval(),
BinOp(eg, Mult, ed) => eg.eval() * ed.eval(),
// ...
}
}
}
Afficher une expression¶
Il peut être utile d'afficher une expression au format "humain". Le trait Debug nous affiche la représentation interne à Rust, mais le trait Display nous permet de définir une représentation humaine.
use std::fmt;
impl fmt::Display for Expression {
fn fmt(&self, f: &mut fmt::Formatter<'_>) -> fmt::Result {
match self {
Const(n) => write!(f, "{}", n),
BinOp(fg, op, fd) => write!(f, "({}{}{})", fg, op, fd),
/* ... */
}
}
}
impl fmt::Display for Binop { /* ... */ }
let e = Expression::BinOp(
Expression::BinOp(
Expression::Const(1),
Plus,
Expression::Const(2)
),
Mult,
Expression::Const(3)
);
println!("{}", e);
affiche ceci
((1+2)*3)
Analyse syntaxique¶
L'analyse syntaxique (parsing) est l'opération qui consiste à reconstruire l'arbre de syntaxe abstraite à
partir de la chaîne de caractères. C'est l'opération inverse de to_string()!
// version simplifiée
trait Parse {
fn parse(s: &str) -> Self;
// contrat de trait: si T:Parse et e:T, alors parse(e.to_string()) == e
}
Une façon de faire cette analyse syntaxique, c'est de définir une grammaire formelle des expressions qui soit non ambigüe (cf cours d'automates du S5), puis appliquer un algorithme permettant de reconstruire l'arbre de dérivation (par exemple l'algorithme CYK que vous avez du voir en cours).
Malheureusement ce n'est pas toujours facile de trouver une grammaire non ambigüe!
Cadeau: on va vous fournir le parser 😅
Boucle Read Eval Print (REPL)¶
C'est le coeur du programme
// version simplifiée
fn main() {
prompt(); // affiche "µRust #"
for line in io::stdin().lock().lines(){ // LOOP
// READ (entrée standard)
let input = line.unwrap();
// PARSE (analyse syntaxique)
let e : Expression = parse(&input);
// EVAL
let n : isize = e.eval();
// PRINT
print!("- : isize = {}\n", n);
prompt() // prochain prompt
}
}
Gestion des erreurs¶
Quand on interprète un programme, il peut se produire des erreurs à plusieurs étapes:
- durant l'analyse syntaxique (fonction
parse) - durant l'évaluation (méthode
eval)
Exemple
µRust # 1 + 2 *
Parse error : cannot parse expression `1 + 2 *`
µRust # 1 / (1 - 1)
Evaluation error : division by 0, 1 - 1 evaluates to 0.
µRust #
On va utiliser le type énuméré Result de Rust pour gérer les erreurs (dans d'autres langages, on
l'aurait fait à l'aide d'exceptions)
// rappel: le type Result de la librairie standard
enum Result<T, E> {
Ok(T),
Err(E),
}
// notre trait Parse, avec la gestion des erreurs
type ParseError = /* .. */
trait Parse {
fn parse(s: &str) -> Result<Self, ParseError>;
}
On aura des types énumérés pour les erreurs qui implémentent Display pour pouvoir afficher des messages d'erreurs.
enum Error {
ParseError(ParseError),
EvalError(EvalError)
}
enum EvalError {
DivisionByZero,
// ...
}
impl Display for Error { /* ... */ }
Voici donc la nouvelle version de notre méthode eval
// version simplifiée
impl Expression {
fn eval(&self) -> Result<isize, EvalError> {
match self {
Const(n) => Ok(n),
// notez le `Ok` pour emballer l'entier
BinOp(eg, PLUS, ed) => Ok(eg.eval()? + ed.eval()?),
// notez le `?` pour déballer l'entier du résultat de `eval`
BinOp(eg, DIV, ed) => {
let (vg, vd) = (eg.eval()? , ed.eval()?);
if (vd == 0) {
Err(DivisionByZero)
} else {
Ok(vg / vd)
}
}
// ...
}
}
}
Et la nouvelle version de notre boucle REPL
// version simplifiée
fn parse_eval(input: &str) -> Result<isize, Error> {
match Expression::parse(input) {
Ok(expr) => expr.eval().map_err(|err| Error::EvalError(err))
Err(e) => Err(Error::ParseError(e)),
}
}
fn main() {
prompt();
for line in io::stdin().lock().lines(){
// READ
let input = line.unwrap();
// PARSE & EVAL
match parse_eval(input) {
// PRINT
Ok(n) => { print!("- : isize = {}\n", n); }
// PRINT ERROR MSG (Error implements `Display`)
Err(err) => { print!("{}", err)}
}
prompt() // prochain prompt
}
}
Les variables : une calculatrice à registres¶
On veut maintenant ajouter la possibilité de sauver des calculs dans des variables. De même qu'en Scheme, on va interdire de redéfinir une variable déjà définie en masquant l'ancienne définition (ce n'est pas interdit en Rust).
µRust # let x = 1 + 1
x : isize = 2
µRust # let y = x + 3 * 4
y : int = 14
µRust # x + y + 1
- : int = 17
µRust # let x = 17
Evaluation error: variable `x` is already defined
µRust # z + 1
Evaluation error: variable `z` is not defined
Chaque déclaration de variable ajoute un couple nom/valeur à l'espace de noms (namespace).
Cet espace de noms permet d'évaluer des expressions arithmétiques qui contiennent des variables.
Si on essaie de déclarer une variable qui existe déjà dans l'espace de noms, on a une erreur (patience, on introduira la mutation plus tard...)
Prise en compte des nouvelles erreurs d'évaluation¶
enum EvalError {
DivisionByZero(Expression),
Undefined(Identifier),
AlreadyDefined(Identifier),
// ...
}
Les identifiants¶
Un identifiant représente un nom de variable. Pour nous il s'agira seulement d'une chaîne de caractères non mutable.
#[derive(Clone, PartialEq, Eq, Hash)]
struct Identifier(Rc<str>)
impl Debug for Identifier { /* ... */ }
impl Display for Identifier { /* ... */ }
impl From<&str> for Identifier { /* ... */ }
// exemple d'utilisation
let id = Identifier::from("x");
print!("{} == {}",&id, &id); // -> x == x
print!("{:?}", &id); // -> "x" avec les guillemets autour de l'identifiant
Les espaces de noms¶
Un espace de noms est une fonction qui associe une valeur (pour le moment, un entier) à un identifiant.
On va représenter cette fonction par une HashMap, et l'enrober dans un struct.
// version simplifiée
struct NameSpace (HashMap<Identifier, isize>)
On aura besoin de deux opérations (pour le moment):
- rechercher une définition : la définition peut ne pas exister
- ajouter une définition (un
let) : peut causer une erreur
// version simplifiée
impl NameSpace {
fn new() -> Self;
fn find(&self, id: &Identifier) -> Result<isize, EvalError> { /* ... */ }
fn declare(&mut self, id: &Identifier, val: isize) -> Result<(), EvalError> { /* ... */ }
}
Ajouter les variables dans la syntaxe¶
On a deux objets syntaxiques: les expressions arithmétiques (Expression), et les instructions (Instruction).
// version simplifiée
enum Expression {
Const(isize),
Var(Identifier),
BinOp(Box<Expression>, Binop, Box<Expression>),
// ...
}
enum Instruction {
Expr(Expression),
Let(Identifier, Expression),
// ...
}
Il faut étendre le parser aux instructions
impl Parse for Instruction {
fn parse(s: &str) -> Result<Self, ParseError> { /* ... */ }
}
Exemple d'utilisation
let instr = Instruction::parse("let x = y + 1");
println!("{:?}", instr);
// affiche
// Instruction::Let("x",
// Expression::BinOp(Expression::Var("x"),
// Binop::PLUS,
// Expression::Const(1))))
Évaluation en présence de variables¶
Voyons maintenant comment évaluer une expression arithmétique contenant des variables.
// version simplifiée
impl Expression {
fn eval(&self, ns: &NameSpace) -> Result<isize, EvalError> {
match self {
Const(n) => Ok( n ),
Var(x) => Ok( ns.find(x)? ),
BinOp(eg, PLUS, ed) => Ok( eg.eval(&ns)? + ed.eval(&ns)? ),
/* ... */
}
}
Exécution d'une instruction¶
Il nous faut maintenant exécuter une instruction: soit on a affaire à une expression, soit à une déclaration de variable.
Dans les deux cas, on voudra afficher la valeur (ou l'erreur), et possiblement le nom de la variable définie.
Dans le cas d'une déclaration de variable, il faut en plus modifier l'espace de noms à l'intérieur de la fonction. On doit donc faire un emprunt mutable de l'espace de nom.
// version simplifiée
impl Instruction {
fn exec(&self, ns: &mut NameSpace)
-> Result<(Option<Identifier>, isize), EvalError>
{
match self {
Expr(e) => {
let v = e.eval(&ns)?;
Ok((None, v))
}
Let(id, e) => {
let v = e.eval(&ns)?;
ns.declare(id, v)?;
Ok(Some(id), v)
}
}
}
}
Nouvelle version de la boucle REPL¶
// version simplifiée
fn main() {
prompt();
let mut ns = NameSpace::new();
for line in io::stdin().lock().lines(){
// READ
let input = line.unwrap();
// PARSE, EVAL, PRINT
match Instruction::parse(&input).exec(&mut ns) {
Ok((Some(id), v)) => println!("{} : isize = {}", id, v),
Ok((None, v)) => println!("- : isize = {}", v),
Err(err) => print!("{}", err),
}
prompt() // prochain prompt
}
}
Et c'est tout, notre interpréteur sait maintenant gérer des variables!
Les booléens et les expressions conditionnelles¶
On veut étendre le langage pour pouvoir manipuler des booléens avec des comparaisons, des opérateurs paresseux, et des expressions conditionnelles
Exemple
µRust # let x = 1 - 1 == 0
x : bool = true
µRust # let y = true || 1 / 0 == 0
y : bool = true
µRust # let z = 1 / 0 == 0
Evaluation error : division by zero
µRust # let t = (x == y) ? 1 : z
t : isize = 1
µRust # let u = (x != y && false) ? 1 : z
Evaluation error : variable `z` is not defined
Il y a plusieurs changements à apporter:
le résultat de l'évaluation n'est plus toujours un entier, cela peut être un booléen. Il va donc falloir introduire un enum
Valuepour représenter la valeur d'une expression. Cette structure comportera deux informations: le type de laValue(déterminé par le constructeur), et la valeur proprement diteon a de nouveaux opérateurs:
==,&&, etc : il va falloir enrichir l'enumBinop.on a des expressions conditionnelles
(...) ? ... : ...: à nouveau, le changement à faire sera dans l'enumExpression
Les Value et les nouvelles Expression¶
// version simplifiée
enum Value {
Bool(bool),
Int(isize),
// ...
}
enum Expression {
Const(Value),
Var(Identifier),
BinOp(Box<Expression>, Binop, Box<Expression>),
Conditional {
cond: Box<Expression>,
cond_true: Box<Expression>,
cond_false: Box<Expression>
},
// ...
}
La suite en TP!
Les blocs d'instructions¶
On veut maintenant pouvoir créer des blocs d'instructions/expressions.
Un bloc a une valeur: c'est la valeur de la dernière instruction/expression qui définit le résultat de l'évaluation du bloc.
Les définitions faites à l'intérieur d'un bloc sont "effacées" à la fin du bloc.
µRust # let x = 1
x : isize = 1
µRust # {let x = 42; x + 1 }
- : isize = 43
µRust # x
- : isize = 1
µRust # {let y = 0}
- : isize = 0
µRust # y
Evaluation Error: Undefined identifier: `y`
Blocs d'instructions imbriqués¶
On peut mettre des blocs dans des blocs.
Exemples
µRust # {let x = 1; {let y = 2; x + y}}
- : isize = 3
µRust # let x = { if true {let z = 1; z } else { 2 }}
x : isize = 1
Règle de localité¶
Chaque bloc d'instructions a son propre espace de nom.
On peut donc avoir deux identifiants identiques qui ont plusieurs définitions, chacune dans son espace de nom.
Règle de localité: les définitions les plus récentes (= les plus internes) masquent les plus anciennes.
µRust # let x = 1
x : isize = 1
µRust # {let x=2; {let x=3; x}}
- : isize = 3
µRust # {let x=2; {let x=3}; x}
- : isize = 2
µRust # x
- : int = 1
Pile des espaces de noms¶
Les espaces de noms forment une pile, avec au sommet l'espace de nom le plus local/récent.
C'est la pile d'appel (sauf qu'ici on n'a pas vraiment d'appel de fonctions... mais c'est l'idée).
Quand on entre dans un nouveau bloc d'instructions, on empile un nouvel espace de nom
Quand on quite le bloc d'instruction, on dépile l'espace de nom au sommet de la pile.
Pour pouvoir visualiser la pile, on va supposer que notre interpréteur µRust dispose d'une instruction spéciale !dump_stack qui affiche l'état de la pile au moment où on l'exécute.
Exemple
µRust # let x = 0
x : isize = 0
µRust # let y = 1
y : isize = 1
µRust # !dump_stack
[x|->0, y|-> 1]
µRust # {let z = 2; {let t = 3; !dump_stack }}
[t|-> 3]
[z|-> 2]
[x|->0, y|-> 1]
µRust # !dump_stack
[x|->0, y|-> 1]
Représentation Rust de la pile µRust¶
On va représenter la pile par un Vec<NameSpace> qu'on enrobe dans un struct pour pouvoir ensuite
y attacher des méthodes.
struct NameSpaceStack { stack: Vec<NameSpace> }
impl NameSpaceStack {
fn new() -> Self { /* ... */ }
fn push(&mut self, ns: NameSpace) { /* ... */ }
fn pop(&mut self) -> Option<NameSpace> { /* ... */ }
}
Remarque: le sommet de la pile est la dernière valeur du vecteur self.stack. C'est là que les méthodes Vec::push et Vec::pop ajoutent ou enlèvent un élément (les tableau extensibles grandissent par la fin...)
Méthode NameSpaceStack::declare¶
Quand on déclare un nouvel identifiant, on le fait dans l'espace de noms qui se trouve au sommet de la pile (celui des variables définies dans le bloc d'instruction courant).
impl NameSpaceStack {
fn declare(&mut self, id: Identifier, v: Value) -> Result<(), EvalError> {
// on récupère l'espace de nom au sommet de la pile
let ns = &mut self.stack[self.stack.len() - 1];
// on y déclare l'identifiant avec sa valeur
ns.declare(id, v);
}
}
Méthode NameSpaceStack::find¶
Quand on cherche la valeur associée à un identifiant dans la pile, on doit appliquer la règle de localité.
On commence par voir si l'identifiant est défini dans l'espace de nom au sommet de la pile.
S'il n'est pas défini au sommet, on continue la recherche dans les espaces de noms qui se trouvent en-dessous, en descendant la pile jusqu'à trouver un espace de nom qui définisse l'identifiant.
impl NameSpaceStack {
fn find(&self, id: &Identifier) -> Result<Value, EvalError> {
// on parcourt la pile de haut en bas
// i.e. le vec de droite à gauche
for ns in self.stack.iter().rev() {
match ns.find(id) {
Ok(v) => return Ok(v),
Err(_) => continue,
}
}
// si on n'a pas trouvé de définition
// après avoir descendu toute la pile,
// on lève une erreur
Err(EvalError::Undefined(id))
}
}
Représentation et exécution des blocs d'instruction¶
// on représente un bloc d'instructions par un vecteur d'instructions
enum Instruction {
Expr(Expression),
Let(Identifier, Expression),
Block(Vec<Instruction>), // note: pas besoin d'un Box<...>
// ...
}
// on exécute les instructions dans l'ordre du bloc
impl Instruction {
fn exec(&self, &mut nss: NameSpaceStack)
-> Result<(Option<Identifier>, Value), EvalError>
{
match self {
// ...
Block(instructions) => {
// on ajoute un nouvel espace de nom à la pile
nss.push(NameSpace::new());
let mut returned_value = /* ???? */ ;
for instr in &instructions {
returned_value = instr.exec(&mut ns)?.1;
};
// on dépile
nss.pop().unwrap();
Ok((None, returned_value))
}
// ...
}
}
}
Bloc d'instructions vide¶
On posera par convention qu'un bloc vide renvoie la valeur spéciale () du type unit.
µRust # { }
- : unit = ()
Il faudra donc ajouter ce type et cette valeur à l'enum Value.
Ce qu'il faut retenir¶
pour représenter une expression arithmétique, ou un programme, on a utilisé un arbre de syntaxe abstraite (AST). C'est un analyseur syntaxique (parser) qui calcule l'AST à partir de la chaîne de caractères.
les espaces de noms associent des valeurs aux identifiants.
la pile d'appel est composée d'espaces de noms. L'espace de nom au sommet de pile contient les définitions du bloc d'instruction le plus interne (les définitions les plus récentes).
la règle de localité : pour chercher la définition associée à un identifiant, on parcours la pile en descendant
En TP tout à l'heure: revoir tout ça et ajouter mutation et boucles!