Paradigmes et interprétation

Programmation logique 1 : Datalog

Une brève, incomplète, histoire des langages de programmation

19e siècle, puis début 20e siècle: naissance de la programmation impérative

• Ada Lovelace programme le calcul des nombres de Bernoulli sur la machine de Babbage
• les canuts programment les métiers Jacquart
• Alan Turing introduit des invariants et écrit une des premières preuves de programmes
• Konrad Suse propose un langage de programmation bi-dimensionel, le Plankalkül

années 60: l'éclosion de la plupart des paradigmes dominants actuels

• John Mac Carthy, avec LISP, fait passer la programmation fonctionnelle de la théorie (le lambda-calcul d'Alonzo Church ) à la pratique
• Grace Hopper participe à la naissance du langage COBOL, le premier langage dédié à l'informatique de gestion
• face à la "programmation spaghetti", Edsger Dijskra ou encore Tony Hoare participent à la conception d'ALGOL) et posent des principes pour une programmation plus structurée, en particulier en programmation concurrente
• Ole-Johan Dahl et Kristen Nygaard font de Simula le premier langage orienté objet

l'histoire continue

• dans les années 70, à Marseille, Alain Colmerauer invente un nouveau paradigme, la programmation logique, qui ouvrira la voie de la programmation par contraintes et des systèmes experts
• dans les années 80, SQL cristalise les idées des multiples langages de requêtes
• dans les années 90, apparaissent les langages du web (HTML/XML, CSS)

Qu'est-ce qu'un programme Prolog?

Un programme Prolog contient trois parties:

• une base de faits, par exemple "Socrate est un homme"
• un ensemble de règles permettant de déduire de nouveaux faits
• une requête permettant d'interroger l'ensemble des faits déductibles à partir de la base et des règles

Comme SQL, c'est donc, en un certain sens, un langage de requête. Mais c'est aussi un vrai langage de programmation qui permet de calculer tout ce qui est calculable (c'est un langage Turing complet).

Et Datalog?

C'est un fragment de Prolog qui n'est pas Turing complet, et qui peut être vu comme un langage de requêtes pour une base de données relationnelle.

Les atomes

Un atome est un prédicat avec des arguments qui sont des constantes ou des variables.

Une constante peut être un nombre (entier ou flottant), un identifiant, ou une chaîne de caractères.

Les prédicats et les identifiants commencent par une lettre en minuscule.

Les variables commencent par une lettre majuscule.

Exemples:

• homme(X) est un atome avec le prédicat homme et la variable X
• temperature(ajourd_hui, "Nice", 22.5) est un atome avec le prédicat temperature et les constantes aujourd'hui, "Nice", et 22.5
• temperature(demain, Ville, T) est un atome avec la constante demain et les variables Ville et T
• temperature(_,_,T) est un atome avec deux variables "anonymes" et la variable T

Le nombre d'arguments d'un prédicat est fixe, c'est son arité, que l'on indique parfois après le nom du prédicat, par exemple homme/1, temperature/3, a/0.

Un atome qui ne contient pas de variable est appelé un atome clos

Exemples:

• temperature(ajourd_hui, "Nice", 22.5) est un atome clos
• a est un atome clos (avec un prédicat d'arité 0)

On utilisera la notation $\mathcal{A}$ pour parler d'un atome, $c$ pour une constante, et $t$ pour un terme: cette semaine, un terme est simplement une constante ou une variable.

La base de faits

C'est une liste d'atomes, chacun terminé par un point.

homme(socrate). homme(platon). temperature(aujourd_hui, "Paris", 13). temperature(demain, "Nice", 26.5). a.

En Prolog, un fait peu utiliser des variables.

Exemple

egal(X,X).

Mais, pour nous dans ce cours, en Datalog, les faits modélisent une base de données relationnelle, et ne comportent pas de variables.

• base de faits $\Leftrightarrow$ base de données relationelle
• predicat $\Leftrightarrow$ table
• fait $\Leftrightarrow$ ligne d'une table

Les règles

Une règle est de la forme $\mathcal{A}$ :- $\mathcal{A}_1, \ldots , \mathcal{A}_n$ où

• $\mathcal{A}$, $\mathcal{A}_1, \ldots, \mathcal{A}_n$ sont des atomes
• $\mathcal{A}$ est la conclusion de la règle
• $\mathcal{A}_1, \ldots, \mathcal{A}_n$ sont les prémisses, autrement dit les hypothèses nécessaires pour pouvoir appliquer la règle.

Toutes les hypothèses doivent être satisfaites pour pouvoir appliquer la règle et déduire la conclusion. Le , a le sens d'une conjonction (le et logique).

Les variables sont quantifiées universellement en début de chaque règle

Exemples

b :- a.  /* si `a` alors `b` */ 


% si `a1` et `a2` et ... et `an`, alors b
b :- a1, a2, ... , an.

% si Socrate est un homme, alors Socrate est mortel.
mortel(socrate) :- homme(socrate).

pour tout X, si X est un homme, alors X est mortel ("tous les hommes sont mortels")

mortel(X) :- homme(X).

Note: cette règle induit la règle précédente et toute autre règle obtenue en remplaçant X par une constante, par exemple

mortel(platon) :- homme(platon).
mortel("Nice") :- homme("Nice").
mortel(13) :- homme(13).

etc.

Pour chaque instanciation possible des variables par une constante, la règle s'applique

Autres exemples de règles

pour tout X, Y, si X est le frère de Y, alors Y est le frère de X.

est_frere(X,Y) :- est_frere(Y,X).

pour tout X, Y, Z, si X est le frère de Y et si Y est le frère de Z, alors X est le frère de Z.

est_frere(X,Z) :- est_frere(X,Y), est_frere(Y,Z).

Note: toutes les variables sont toujours universellement quantifiées "en tête". Cependant, les variables qui n'apparaissent pas dans la conclusion (ex: Y ci-dessus) peuvent être perçues comme "existentiellement quantifiées"... mais pas en tête! Tout dépend de là où on place les parenthèses. C'est une équivalence logique que vous devez connaitre: l'énoncé

pour tout X, ( si a(X) alors b )

est équivalent logiquement à l'autre énoncé

si (il existe X tel que a(X)) alors b

$$ \forall X \big(a(X) \Rightarrow b\big)\qquad\Leftrightarrow\qquad \big(\exists X. a(X)\big)\Rightarrow b $$

"X est mortel s'il existe un jour où il meurt"

mortel(X) :- meurt(J, X)

(on aurait pu écrire _ au lieu de J)

Dernier exemple: "à Nice la température est toujours agréable"

agreable(T) :- temperature(_, "Nice", T)

Exercice 1

Écrire des règles Prolog qui correspondent aux règles en langage naturel suivantes:

1. si un jour la température à Paris est agréable, alors ce jour-là la température à Nice est agréable.

2. si un jour la température est la même à Paris et à Nice, alors ce jour-là la température est agréable.

On utilisera les prédicats agreable/1 (propriété d'une température) et temperature/3 (relation entre un jour, un lieu, et une température).

Solution

/* 
si un jour la température à Paris est agréable, 
ce même jour la température à Nice est agréable.
*/

agreable(TNice) :- temperature(J, "Paris", TParis), temperature(J, "Nice", TNice), agreable(TParis)


/*
si un jour la température est la même à Paris et à Nice, ce jour-là la température est agréable.
*/

agreable(T) :- temperature(J, "Paris", T), temperature(J, "Nice", T)

Les requêtes

Une requête est un atome précédé du symbole ?-.

Exécuter un programme Prolog, c'est évaluer une requête. Il y a en général une seule requête dans tout le programme.

Si la requête est un atome clos, le programme termine en disant si cet atome est déductible de la base de faits et des règles, ou s'il n'est pas déductible.

homme(socrate).
mortel(X) :- homme(X).
?- mortel(socrate).

répond true (sur SWISH Prolog, au moins)

homme(socrate).
mortel(X) :- homme(X).
?- mortel(zeus).

répond false

Si la requête est un atome qui n'est pas un clos, l'évaluation va chercher à remplacer les variables par des constantes de sorte à obtenir un atome clos déductible.

homme(socrate).
mortel(X) :- homme(X).
?- mortel(Y)

répond Y=socrate

Une requête peut avoir zéro, une, ou plusieurs solutions. L'évaluation du programme permet de calculer toutes les solutions, parfois en demandant à l'utilisateur de confirmer qu'il veut continuer la recherche après chaque nouvelle solution trouvée.

homme(socrate).
homme(platon).
mortel(X) :- homme(X).
?- mortel(Y).

répond Y=socrate puis Y=platon

homme(socrate).
homme(platon).
dieu(zeus).
demi_dieu(X) :- homme(X), dieu(X).
?- demi_dieu(Y).

répond fail (pas de solution)

Notion de substitution close

Si la requête contient plusieurs variables, une solution fixe une valeur pour chacune des variables.

temperature(hier,"Nice",19.5).
temperature(aujourd_hui,"Paris", 10.2).
temperature(demain,"Nice", 20.3).
?- temperature(Jour,"Nice",T)

renvoie deux solutions:

1. Jour=hier, T=19.5
2. Jour=demain, T=20.3

que l'on notera par la suite [Jour $\leftarrow$ hier, T $\leftarrow$ 19.5] et [Jour $\leftarrow$ demain, T $\leftarrow$ 20.3]

Une solution est une fonction partielle des variables vers les constantes. C'est un objet tellement important que cela porte un nom: une solution est une substitution close.

Le résultat d'un programme Prolog est un ensemble de substitutions (pas forcément closes, cf plus loin)

• $\{$[Jour $\leftarrow$ hier, T $\leftarrow$ 19.5], [Jour $\leftarrow$ demain, T $\leftarrow$ 20.3]$\}$ est l'ensemble des substitutions calculées par le programme ci-dessus
• false et fail correspondent à l'ensemble vide $\emptyset$ (pas de substitution qui soit solution)
• true correspond à l'ensemble contenant la substitution identité (i.e. la substitution de domaine vide): true = $\{[]\}$

Notion de terme

En Datalog, un terme est une constante ou une variable (ce sera plus compliqué en Prolog). On notera $t$ pour un terme.

Notion de substitution

Une substitution est une généralisation des substitutions closes: à une variable, la substitution associe un terme.

Exemple: [$J\leftarrow hier, T\leftarrow T2, T2\leftarrow T3, T3\leftarrow T2 $] est une substitution.

L'ensemble des variables modifiées par la substitution est le domaine de la substitution.

On notera $\mathsf{dom}(\sigma)$ le domaine de la substitution $\sigma$.

On peut appliquer une substitution à un atome: on remplace chaque variable du domaine de la substitution par le terme associé. Les autres variables restent inchangées.

On note $\mathcal{A}[\vec X\leftarrow\vec t]$ le résultat de l'application de la substitution $[\vec X\leftarrow\vec t]$ à l'atome $\mathcal{A}$.

Exemples:

• temperature(J,"Nice",T)[J $\leftarrow$ hier, T $\leftarrow$ T2] = temperature(hier,"Nice",T2)

• temperature(J,"Nice",T)[J $\leftarrow$ hier, T2 $\leftarrow$ 22.5] = temperature(hier,"Nice",T)

Remarque: si $\sigma$ une substitution close, et si toutes les variables de l'atome $\mathcal{A}$ sont dans $\mathsf{dom}(\sigma)$, alors $\mathcal{A}\sigma$ est un atome clos.

On peut composer deux substitutions: si $\sigma_1$ et $\sigma_2$ sont deux substitutions, $\sigma_1;\sigma_2$ est la substitution qui à X associe (X$\sigma_1$)$\sigma_2$.

Exemples:

• $[X\leftarrow 1];[Y\leftarrow 2] = [X\leftarrow 1, Y\leftarrow 2]$
• $[X\leftarrow 1];[X\leftarrow 2] = [X\leftarrow 1]$
• $[X\leftarrow Y];[Y\leftarrow 2] = [X\leftarrow 2, Y\leftarrow 2]$

Déduction d'un atome à partir d'une règle et d'autres atomes

Soit $\sigma$ une substitution.

À partir de la règle

$\mathcal{A}$ :- $\mathcal{A}_1,\ldots\mathcal{A}_n$

et des atomes $\mathcal{A}_1\sigma,\ldots\mathcal{A}_n\sigma$, je peux déduir l'atome $\mathcal{A}\sigma$.

Exemple: je peux déduire demi_dieu(achile) à partir de la règle

demi_dieu(X) :- homme(X), dieu(X)

et des atomes homme(achile) et dieu(achile). J'utilise pour cela la substitution [$X\leftarrow$ achile].

Exercice 2

Calculez l'ensemble de tous les atomes clos déductibles à partir d'une règle et des faits de base pour le programme suivant. Indiquez à chaque fois la règle et la substitution utilisée.

a(1,2,1).
a(1,2,3).
a(Y,X,X) :- a(X,Y,X).
a(2,X,X) :- a(X,Y,Z), b(Y,Z).
b(2,1).
b(X,X) :- a(X,Y,Z), b(Y,Z).
c :- a(X,Y,Z), b(T,U), b(U,T).

Solution

• a(2,1,1) avec la règle a(Y,X,X) :- a(X,Y,X) et la substitution [X $\leftarrow$ 1, Y $\leftarrow$ 2]
• a(2,1,1) avec la règle a(2,X,X) :- a(X,Y,Z), b(Y,Z) et la substitution [X $\leftarrow$ 1, Y $\leftarrow$ 2, Z $\leftarrow$ 1]
• b(1,1) avec la règle b(X,X) :- a(X,Y,Z), b(Y,Z) et la substitution [X $\leftarrow$ 1, Y $\leftarrow$ 2, Z $\leftarrow$ 1]

On ne peut rien déduire immédiatement de la règle c :- a(X,Y,Z), b(T,U), b(U,T) (on pourrait déduire c si on avait le fait b(1,1). dans la base de fait)

Ensemble des atomes déductibles d'un programme Datalog

Définition Un atome est déductible si:

• ou bien c'est un fait de la base de faits
• ou bien il y a une règle qui permet de déduire cet atome à partir d'autres atomes déductibles

C'est donc une définition "par récurrence" sur le nombre d'"étapes de déduction". À chaque étape, on a un ensemble de atomes déductibles, et on applique une règle pour déduire un nouvel atome déductible.

Exemple: dans l'exercice précédent, l'atome c est déductible du programme en deux étapes de déduction, avec comme atome déductible intermédiaire b(1,1).

Dans le cas d'un programme Datalog, l'ensemble des atomes clos déductibles est fini (pourquoi?). Ce ne sera plus le cas la semaine prochaine avec Prolog...

Avancé: atomes non clos déductibles d'un programme

Si tous les faits sont des atomes clos (comme on l'a supposé plus haut pour notre Datalog), les seuls atomes déductibles sont des atomes clos.

Mais si on autorise des faits avec des variables, comme en Prolog, ce n'est plus le cas.

Exemple:

plus_petit(X,X).
egal(X,Y) :- plus_petit(X,Y), plus_petit(Y,X).

Alors l'atome egal(X,X) est déductible par la substitution [X $\leftarrow$ Y].

Si on lance la requête ?- egal(X,Y) sur ce programme, Prolog répond [X $\leftarrow$ Y]. En Prolog, l'ensemble des solutions d'une requête n'est donc pas forcément limité à des substitutions closes.

Faisons le point

On a vu que

• un programme Datalog (resp. Prolog) $P$, sans requête, définit un ensemble fini $A(P)$ d'atomes clos (resp. d'atomes) déductibles
• une requête -?$\mathcal{A}$ génère l'énumération d'une suite finie (resp. dénombrable) $\sigma_1,\sigma_2,\ldots$ de substitutions closes (resp. de substitutions) "qui couvre" l'ensemble des "solutions" de la requête

On peut maintenant préciser le sens du mot "solution": si on applique une substitution $\sigma_i$ à la requête $\mathcal{A}$, on obtient un atome déductible, i.e. $\mathcal{A}\sigma_i\in A(P)$

On peut aussi préciser le sens de "qui couvre": si $\mathcal{A}\sigma$ est déductible, alors $\sigma$ appartient à l'énumération des solutions.

En résumé: $A(P) = \{\mathcal{A}\sigma_1,\mathcal{A}\sigma_2,\ldots\}$

Remarque: l'énumération $\mathcal{A}\sigma_1,\mathcal{A}\sigma_2,\ldots$ peut contenir des répétitions (cf Exercice 2, le fait a(2,1,1) déductible de deux façons)

Comment calculer une solution?

Pour un programme $P$ et une requête ?-$\mathcal{A}$ donnés, on pourrait imaginer de calculer l'ensemble $A(P)$ de tous les atomes déductibles, puis de l'énumérer jusqu'à trouver un atome de la forme $\mathcal{A}\sigma$ pour un certain $\sigma$. Mais on calculerait possiblement beaucoup d'atomes inutiles.

On va s'intéresser à une approche différente, qui est celle standardisée par Prolog (Datalog n'a pas de technique "standard"), et qui permet, en quelque sorte, de n'énumérer "que ce qui est nécessaire" de $A(P)$ pour évaluer la requête ?-$\mathcal{A}$.

Le principe général est le suivant: on "réécrit" la requête jusqu'à arriver à une requête triviale. Au cours de la réécriture, on va manipuler des requêtes contenant plusieurs atomes, de la forme ?- $\mathcal{A}_1,\ldots,\mathcal{A}_n$. L'atome en tête de requête $\mathcal{A}_1$ est celui qu'on va chercher à "éliminer" en premier. Pour ce faire, on va choisir un fait ou une règle qui permet de déduire cet atome, et réécrire la requête.

Cas 1: élimination de la tête de requête grâce à un fait

• requête courante: ?- $\mathcal{A}_1,\ldots,\mathcal{A}_n$
• ma base de faits contient $\mathcal{A}_1'$ qui me permet de prouver un cas particulier de $\mathcal{A}_1$: je peux trouver une substitution $\sigma$ telle que $\mathcal{A}_1' = \mathcal{A}_1\sigma$
• je réécris ma requête en éliminant $\mathcal{A}_1$ et en applicant la substitution: ma nouvelle requête est ?-$\mathcal{A}_2\sigma,\ldots,\mathcal{A}_n\sigma$

Exemple: soit le programme suivant

a(1,2).
a(X,Y) :- a(Y,X), b(X).
b(2).
?- a(X,Y), b(Y), a(Y,Z), b(Y)

Grâce au fait a(1,2), je peux réécrire ma requête comme suit (j'utilise la substution $\sigma=$[X $\leftarrow$ 1, Y $\leftarrow$ 2]):

?- b(2), a(2,Z), b(2).

Grâce au fait b(2), je peux ensuite réécrire ma requête comme suit:

?- a(2,Z), b(2).

et là je ne peux pas éliminer la tête de requête grâce à un fait... il va me falloir utiliser la règle.

Cas 2: réécriture de la tête de requête grâce à une règle

• requête courante: ?- $\mathcal{A}_1,\ldots,\mathcal{A}_n$
• mon programme contient une règle $\mathcal{A}_1'$ :- $u_1,\ldots,u_m$ (à renommage de variables près) qui me permet de prouver un cas particulier de $\mathcal{A}_1$: je peux trouver une substitution $\sigma$ telle que $\mathcal{A}_1'\sigma = \mathcal{A}_1\sigma$. On dit que $\mathcal{A}_1$ et $\mathcal{A}_1'$ sont unifiables, et $\sigma$ est appelé un unificateur (on en reparle après).
• je réécris ma requête en remplaçant $\mathcal{A}_1$ par $u_1,\ldots, u_n$, et en applicant la substitution: ma nouvelle requête est ?-$u_1\sigma,\ldots,u_m\sigma,\mathcal{A}_2\sigma,\ldots,\mathcal{A}_n\sigma$

Exemple: toujours le même programme, avec la requête là où on l'avait laissée:

a(1,2).
a(X,Y) :- a(Y,X), b(X).
b(2).
?- a(2,Z), b(2).

j'utilise la seule règle du programme pour réécrire ma requête comme suit (avec la substitution [X$\leftarrow$ 2, Y $\leftarrow$ Z]):

?- a(Z,2), b(2), b(2).

et je peux alors réécrire ma requête jusqu'à éliminer tous les atomes, grace aux faits a(1,2) et b(2). Je termine sur la requête vide ?-. et j'obtiens la solution [X $\leftarrow$ 1, Y $\leftarrow$ 2, Z $\leftarrow$ 1] à ma requête initiale, qui était ?- a(X,Y), b(Y), a(Y,Z), b(Y).

Arbre de recherche

Pour réécrire la requête, j'ai dû faire des choix:

• choisir un fait ou une règle
• choisir une substitution (un unificateur)

La recherche de solution par réécriture de requête définit donc un arbre de recherche dont les noeuds sont les requêtes avec un nombre arbitraires d'atomes que l'on peut obtenir par réécriture. Chaque chemin dans l'arbre correspond à une stratégie de réécriture.

Le nombre de choix possibles pour un fait ou une règle est fini, puisque mon programme est fini: on peut donc explorer toutes les possibilités.

De même, le nombre de choix possible pour un unificateur est fini à renommage des variables près; il y a même en fait un seul choix le plus général que l'on peut calculer à chaque étape (on en rediscutera).

En résumé, l'arbre de recherche est à branchement fini (c'est même un arbre fini en Datalog), et Prolog va explorer toutes branches de cet arbre pour calculer toutes les solutions.

On étiquette les arètes de l'arbre avec le fait ou règle choisi pour faire la réécriture, ainsi que la substitution que ce choix a induit.

Les feuilles de l'arbre qui contiennent la requête vide sont les feuilles de succès, qui correspondent à une solution.

Pour une feuille de succès accessible depuis la racine par un chemin étiqueté par la suite de substitutions $\sigma_1,\ldots,\sigma_n$, la solution de cette feuille est la substitution composée $\sigma_1;\ldots;\sigma_n$, restreinte aux variables de la requête initiale.

Exemple: soit le programme suivant (on numérote les lignes par comodité)

1. a(1,1).
2. a(2,2).
3. b(X,Y) :- a(X,X), a(Y,Y), a(X,Y).
4. ?- b(Z,T). 

L'arbre de recherche correspond à

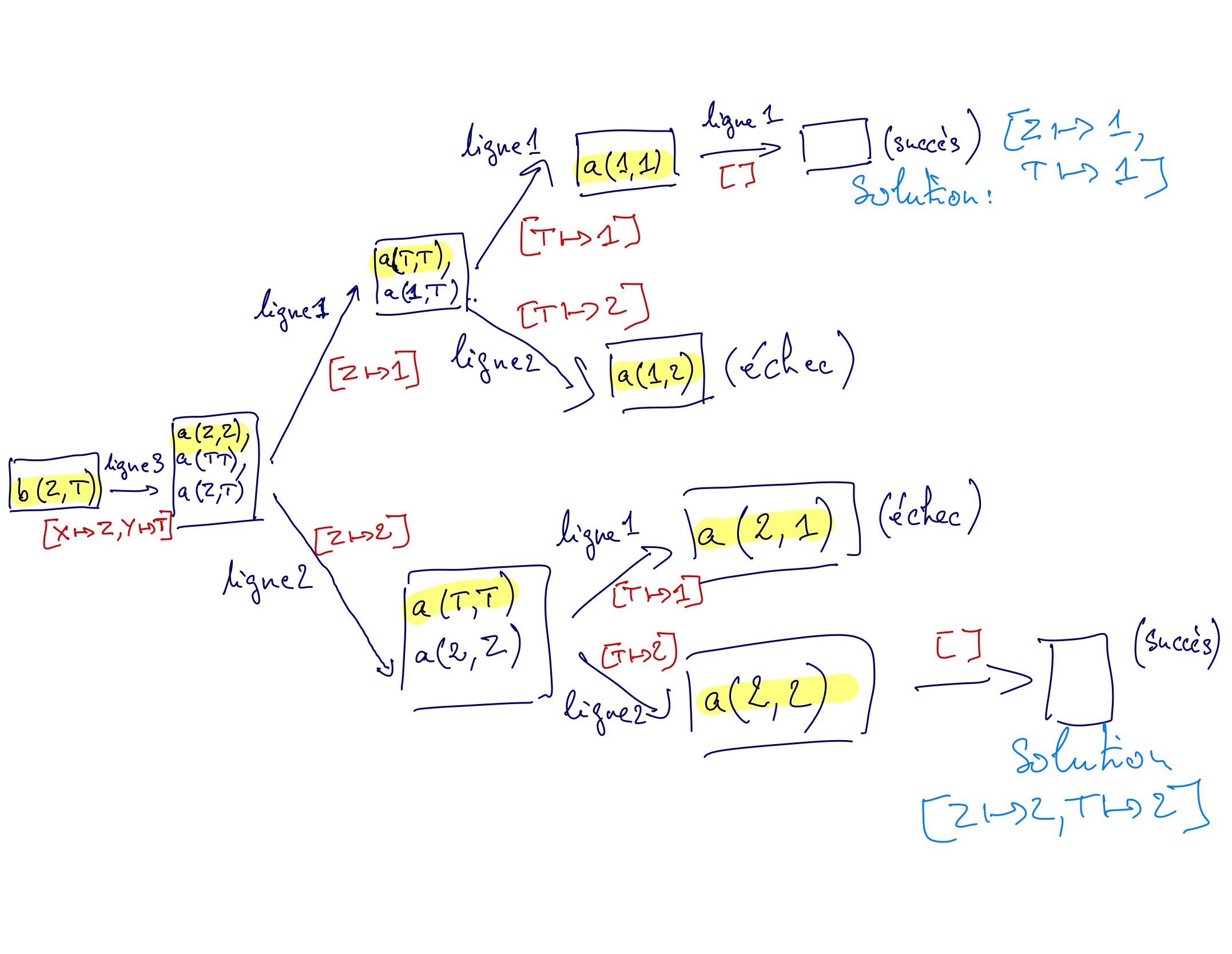
typo: a(2,T) au lieu de a(2,Z) dans le fils de ligne 2.

Exercice 3

Quelles sont les solutions renvoyées par ce programme? Détaillez l'arbre de recherche.

a(1,1).
a(1,2).
a(2,1).
a(2,X) :- a(X,1), a(1,X).
?- a(X,X).

Stratégie d'exploration de Prolog

Prolog explore l'arbre de recherche en profondeur d'abord (depth-first). De plus, il énumère les choix dans l'ordre du programme (les premières lignes en premier).

Exemple: sur l'exemple précédent, Prolog trouve donc d'abord la solution [Z $\leftarrow$ 1, T $\leftarrow$ 1], puis la solution [Z $\leftarrow$ 2, T $\leftarrow$ 2].

On peut avoir des branches infinies et donc partir dans une exploration sans fin et "rater" des solutions. Il est donc important de bien choisir l'ordre dans lequel on écrit les faits et les règles.

Note: Prolog impose d'ailleurs de grouper tous les faits et règles d'un même prédicat les uns à la suite des autres. Par exemple, ce programme n'est pas accepté.

a(1).
a(X) :- b(X,X)
b(1,2) 
a(Y) :- c(Y,Y,Y)

Quelques mots sur l'unification

Le problème de l'unification est le suivant:

• étant donnés deux atomes $\mathcal{A}$ et $\mathcal{A}'$
• trouver un unificateur $\sigma$ "le plus général possible" tel que $\mathcal{A}\sigma=\mathcal{A}'\sigma$

On aura l'occasion d'étudier ce problème en détail pour Prolog plus tard, pour aujourd'hui on s'intéresse uniquement à ce dont on a besoin pour Datalog, et un algorithme par récurrence sera suffisant.

MGU($\mathcal{A}$, $\mathcal{A}'$):

• si $\mathcal{A}$ et $\mathcal{A}'$ ne sont pas basés sur le même prédicat, il n'y a pas d'unificateur
• sinon c'est que $\mathcal{A}$=pred($t_1,\ldots,t_n$), $\mathcal{A}'$=pred($t_1',\ldots,t_n')$, avec les $t_i$ qui sont des constantes ou des variables
• si $\mathcal{A}=\mathcal{A}'$, l'unificateur le plus général est la substitution identité, i.e []
• sinon il existe $i$ tel que $t_i\neq t_i'$
• si $t_i$ est une variable $X_i$, soit $\sigma=$ MGU($\mathcal{A}[X_i \leftarrow t_i']$, $\mathcal{A}'[X_i\leftarrow t_i']$) (s'il existe); alors l'unificateur le plus général de $(\mathcal{A},\mathcal{A}')$ est [$X_i \leftarrow t_i$];$\sigma$
• si $t_i'$ est une variable $X_i$, soit $\sigma=$ MGU($\mathcal{A}[X_i\leftarrow t_i]$, $\mathcal{A}'[X_i\leftarrow t_i]$) (s'il existe); alors l'unificateur le plus général de $(\mathcal{A},\mathcal{A}')$ est [$X_i \leftarrow t_i$];$\sigma$
• sinon $t_i$ et $t_i'$ sont deux constantes distinctes: il n'existe pas d'unificateur

Avancé: en quoi le MGU est "le plus général"

Cet algorithme renvoie un unificateur "le plus général possible" dans le sens suivant:

• si $\sigma_1=$ MGU($\mathcal{A},\mathcal{A}'$) est l'unificateur calculé par l'algorithme, et
• si $\mathcal{A}\sigma_2=\mathcal{A}'\sigma_2$ est un autre unificateur de $(\mathcal{A},\mathcal{A}')$,
• alors il existe $\sigma_{12}$ tel que $\sigma_2=\sigma_1;\sigma_{12}$, autrement dit, $\sigma_2$ est "identique à renommage près" à $\sigma_1$, ou "c'est un cas particulier de" $\sigma_1$ strictement moins général que $\sigma_1$.

On peut aussi expliquer la notion de "plus général possible" en considérant l'ensemble des instances closes d'un atome:

Exemple: en supposant qu'on a 2 constantes 1 et 2,

• les instances closes de a(X,X,Y) sont a(1,1,1), a(1,1,2), a(2,2,1) et a(2,2,2)
• les instances closes de a(Z,T,T) sont a(1,1,1), a(1,2,2), a(2,1,1) et a(2,2,2)
• les instances closes communes aux deux sont donc a(1,1,1) et a(2,2,2)
• ce sont les instances closes de MGU(a(X,X,Y),a(Z,T,T)) = a(X,X,X) ( = a(Z,Z,Z) = a(U,U,U) ) Plus généralement, le MGU de $\mathcal{A}_1$ et $\mathcal{A}_2$ est l'atome qui permet de "couvrir" l'ensemble des instances closes communes à $\mathcal{A}_1$ et $\mathcal{A}_2$.

Pour ceux qui ne sont pas trop fachés avec les maths: l'ensemble des atomes, quotienté par la relation d'équivalence "à renommage près", forme un treillis, pour la relation d'ordre "être instance de", qui se plonge dans le treillis des ensembles d'atomes clos. ouf!

Exercice 4

Calculer le MGU, lorsqu'il existe, des couples d'atomes suivants:

1. a(X,1) et b(1,Y)
2. a(X,1,X,Y) et a(2,Z,T,T)
3. a(X,1,X) et a(2,Y,Y)

Solution

1. pas de MGU, le prédicat est différent
2. On a le calcul suivant

MGU(a(X,1,X,Y), a(2,Z,T,T)) = [X <- 2]; MGU(a(2,1,2,Y), a(2,Z,T,T))
                            = [X <- 2];[Z <- 1]; MGU(a(2,1,2,Y), a(2,1,T,T))
                            = [X <- 2];[Z <- 1];[T <- 2]; MGU(a(2,1,2,Y), a(2,1,2,2))
                            = [X <- 2];[Z <- 1];[T <- 2];[Y <- 2]
                            = [X <- 2, Z <- 1, T <- 2, Y <- 2]

3. On a le calcul suivant

MGU(a(X,1,X), a(2,Y,Y)) = [X <- 2]; MGU(a(2,1,2), a(2,Y,Y))
                        = [X <- 2];[Y <- 1]; MGU(a(2,1,2), a(2,1,1))
                        = echec

Renommage des variables (Exercice 5)

On a mentionné en passant, dans le cas 2 "réécriture de requête par application de règle", qu'on pouvait utiliser une règle "à renommage des variables près".

Est-ce que vous voyez pourquoi on a le droit? et pourquoi c'est parfois nécessaire de renommer les variables?

Donnez un exemple où le renommage des variables est nécessaire pour trouver un unificateur.

Solution On a le droit de renommer les variables d'une règle puisque ces variables sont quantifiées universellement :

$\forall \vec{X}. a_1(\vec{X})\wedge\ldots\wedge a_n(\vec{X})\Rightarrow a(\vec{X})$ est logiquement équivalent à $\forall \vec{Y}. a_1(\vec{Y})\wedge\ldots\wedge a_n(\vec{Y})\Rightarrow a(\vec{Y})$

Pour comprendre pourquoi c'est nécessaire, considérons le programme ci-dessous

a(1,0).
a(X,1) :- a(1,X).
-? a(0,X).

L'atome $a(0,1)$ est déductible par l'atome $a(1,0)$ et la règle. Il y a donc une solution qui est [X $\leftarrow$ 1] (c'est d'ailleurs la seule solution).

Si on essaie de réécrire la requête ?-a(0,X) en appliquant la règle et sans renommer les variables, on doit unifier a(X,1) et a(0,X): il n'y a pas d'unificateur!

Par contre, si on renomme la variable X dans la règle, par exemple si on utilise la règle

a(X',1) :- a(1,X')

alors on doit unifier a(X',1) et a(0,X), on trouve l'unificateur [X' $\leftarrow$ 0, X $\leftarrow$ 1], et on peut réécrire la requête en

-? a(1,0)

et terminer au coup suivant par application du fait a(1,0).

La coupure

Tout langage de programmation a ses déroutements qui permettent de modifier le déroulement attendu du programme.

• le goto (C, Basic, ...)
• le setjmp/longjmp (C)
• le callcc (Lisp)
• break, continue, return
• les exceptions,...

... et en Prolog, le déroutement s'appelle "la coupure". Comme tout déroutement, il est un peu déroutant!

La coupure, aussi appelée "cut", est un atome particulier noté !. Comme son nom l'indique, la coupure sert à "couper" des branches de l'arbre de recherche.

La coupure est un atome sans signification logique, toujours "déductible", mais éliminer ! de la requête a pour effet de bord de modifier l'arbre de recherche: au moment où on élimine !, on coupe l'ensemble des branches en attente créées depuis la réécriture qui a introduit la coupure.

Exemple 1 : soit le programme suivant (on numérote les lignes par comodité)

1. a(1,1).
2. a(2,2).
3. b(X,Y) :- a(X,X), a(Y,Y), a(X,Y), !.
4. ?- b(Z,T). 

L'arbre de recherche correspond à

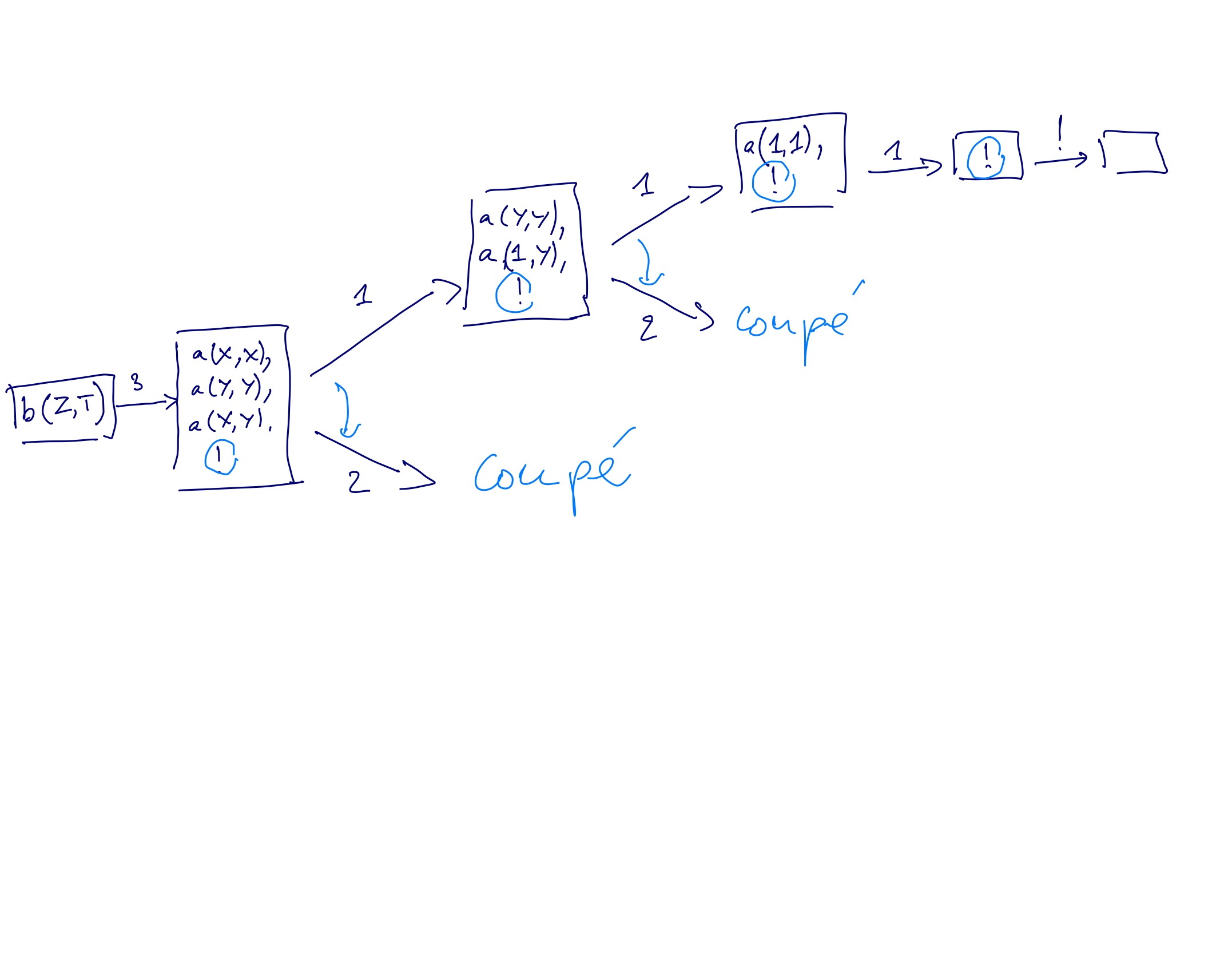
Exemple 2 : soit le programme suivant (on numérote les lignes par comodité)

1. a(1,1).
2. a(2,2).
3. b(X,Y) :- a(X,X), ! , a(Y,Y), a(X,Y).
4. ?- b(Z,T). 

L'arbre de recherche correspond à

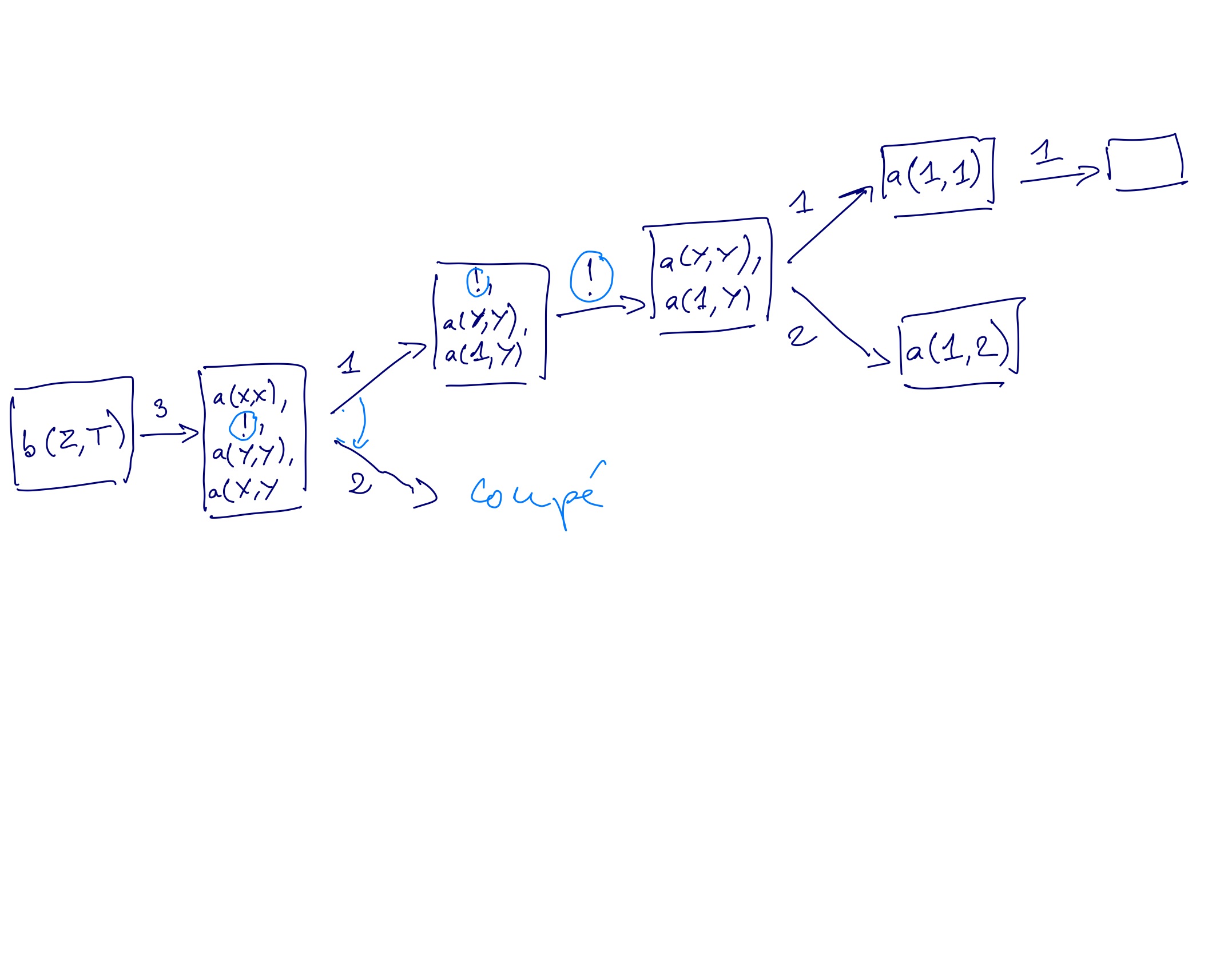
Exemple 3 : soit le programme suivant (on numérote les lignes par comodité)

1. a(1,2).
2. a(X,Y) :- a(Y,X), !.
3. a(3,4).
4. b(Z) :- a(Z,T).
5. b(5).
6. ?- b(U). 

L'arbre de recherche correspond à

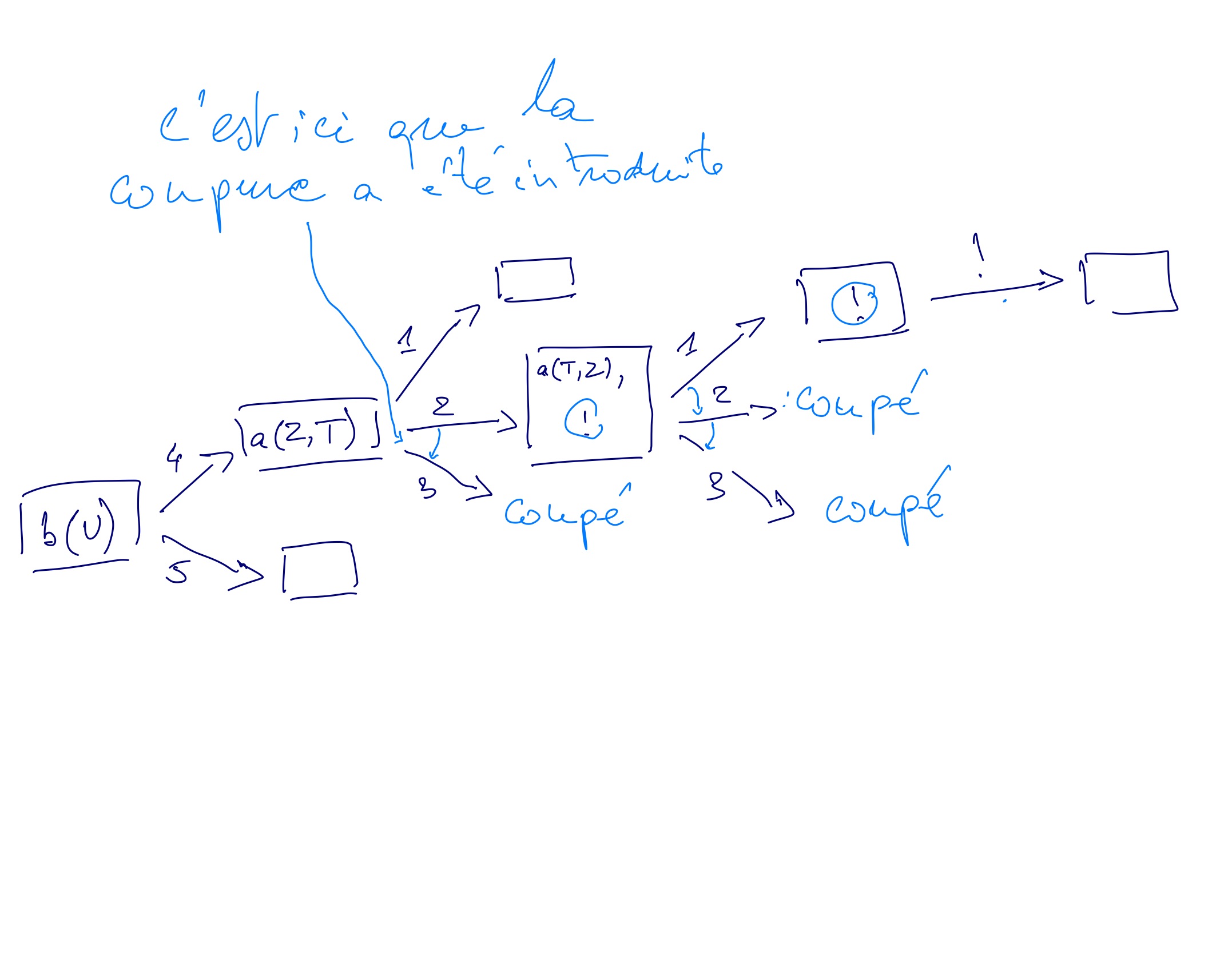
À suivre...

En TP:

• exemples de programmes Datalog
• exemples d'utilisation de la coupure

La semaine prochaine: on termine l'interpréteur microrust!