Rappel de la semaine dernière¶
on a étudié un fragment de Prolog appelé Datalog
un programme est constitué de faits (ex:
homme(socrate)., de règles (ex:mortel(X) :- homme(X)., et de requêtes (ex:?- mortel(socrate).)un atome est un prédicat qui exprime une propriété d'un terme (ex:
mortel(socrate)) ou une relation entre plusieurs termes (ex:fils_de(zeus, X))socrate,zeus,3.14,"hello, world!"sont des constantes, etX,Y,Z,... sont des variables.
Les termes¶
La semaine dernière, nous avons supposé qu'un terme était soit une constante, soit une variable. Cette semaine nous allons donner la véritable définition d'un terme.
Définition (terme)
- une variable est un terme
- si $t_1,\ldots,t_n$ sont des termes, et si $f$ est un symbole de fonction d'arité $n\geq 0$, alors $f(t_1,\ldots, t_n)$ est un terme
En particulier, une constante (qui est un symbole de fonction d'arité 0) est un terme.
Exemples:
pere(X)est un terme formé avec le symbole de fonctionpere/1temperature(J, "Nice")est un terme formé avec le symbole de fonctiontemperature/2.
Comme son nom l'indique, un symbole de fonction sert à modéliser une relation fonctionnelle:
- un individu peut avoir 0, 1 ou plusieurs fils:
fils_dese modélise naturellement comme une relation binaire - un individu a un unique père, la relation
pere_deest fonctionnelle, et se modélise naturellement par un symbole de fonction - idem, la température à un instant donné en un lieu donné est "unique", et la relation "température" est une relation fonctionnelle
La semaine dernière on écrivait en Datalog:
agreable(T) :- temperature(J,"Nice",T)
pour modéliser l'énoncé "à Nice la température est toujours agréable". On avait modélisé la relation "température" par un prédicat. Cependant, comme cette relation est fonctionnelle, en Prolog on va pouvoir la modéliser par un symbole de fonction, et modéliser l'énoncé ci-dessus ainsi
agreable(temperature(J,"Nice")).
Si on veut modéliser l'énoncé "si un jour la températurature est agréable à Paris, alors ce même jour elle l'est aussi à Nice", on écrira
agreable(temperature(J,"Nice")) :- agreable(temperature(J,"Paris")).
etc
Les termes sont des objets purement symboliques, au sens où les symboles de fonction n'ont aucune interprétation prédéfinie et ne s'"évaluent" pas.
- Exemple:
pere(athena)etzeussont deux termes distincts.
Un terme n'est ni plus ni moins qu'un arbre étiqueté dont les feuilles peuvent contenir des variables.
- Exemple: le terme
temperature(J,prefecture("06"))n'est rien d'autre que l'arbre
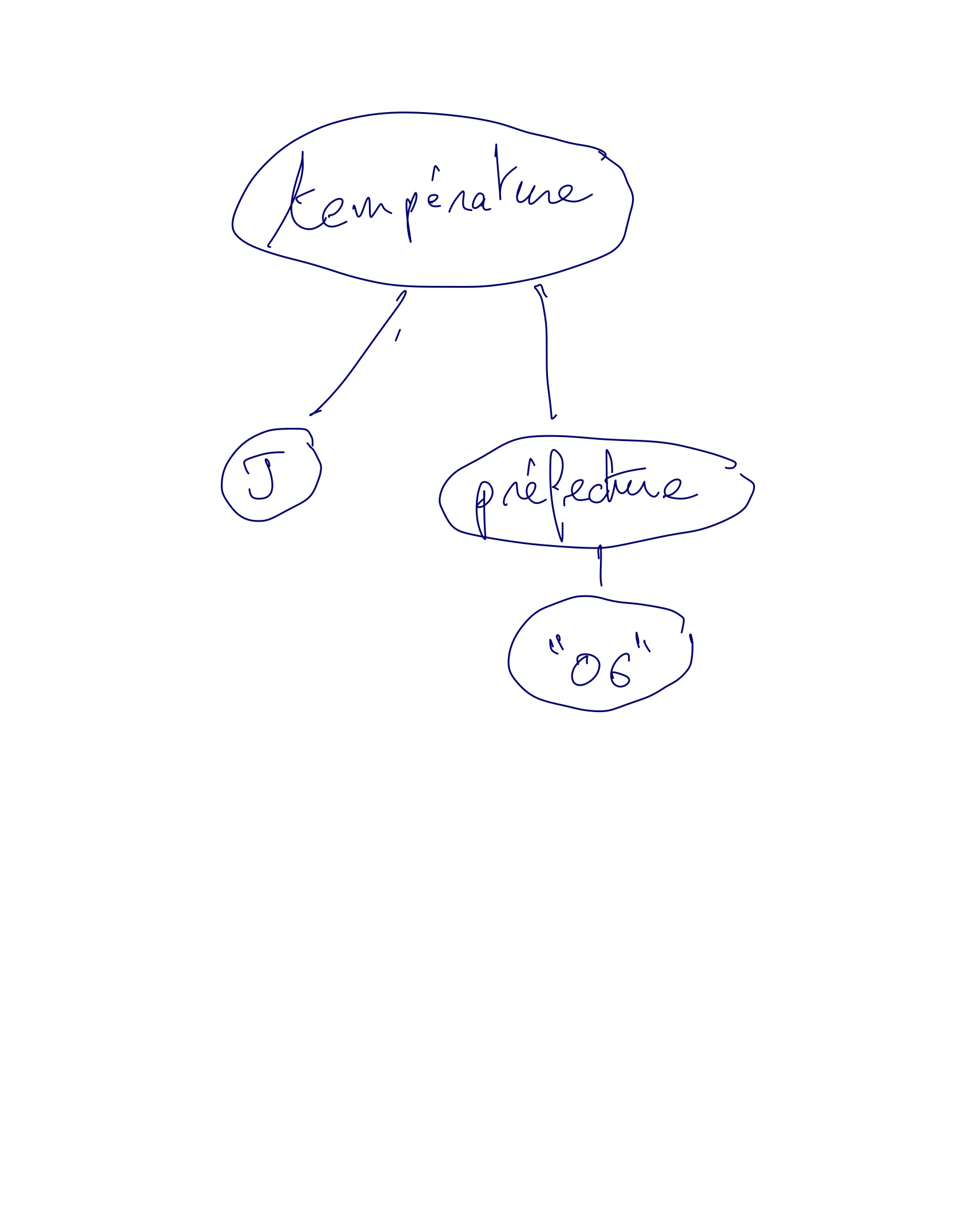
Deux termes $t_1$ et $t_2$ sont égaux, ce que l'on notre $t_1=t_2$, si $t_1$ et $t_2$ sont le même arbre étiquetté (à isomorphisme près).
Usage des symboles de fonction dans les programmes Prolog¶
On peut écrire des règles et des requêtes qui contiennent des symboles de fonction, et utiliser Prolog pour faire du calcul symbolique.
Exemple: calculer le prédécesseur de 2¶
egaux(X,X).
?- egaux(successeur(X), successeur(successeur(zero)))
Ce programme renvoie [X <- successeur(zero)].
Cette façon de représenter un entier par un terme à l'aide des symboles zero/0 et successeur/1 est parfois appellée la représentation de Peano, ou "entiers unaires".
Autre exemple¶
On peut "axiomatiser l'addition":
egaux(add(zero,X)), X).
egaux(add(succ(X),Y), succ(Z)) :- egaux(add(X,Y), Z).
et ensuite faire une requête qui calcule la soustraction 2-1 en résolvant l'équation "1+X=2"
?- egaux(add(succ(zero),X), succ(succ(zero))).
Pratique courante: utiliser un prédicat pour représenter une relation fonctionnelle. Cela permet de se passer du prédicat "egaux".
Ici cela donne:
add(zero, X, X).
add(succ(X), Y, succ(Z)) :- add(X, Y, Z).
?- add(succ(zero), X, succ(succ(zero)))
Les listes chaînées¶
On peut modéliser une liste chaînée à l'aide des symboles de fonction cons/2 et nil/0:
- la liste vide s'écrit
nil - la liste [1,2,3] s'écrit
cons(1,cons(2,cons(3,nil)))
On peut axiomatiser ce qu'est la concaténation de deux listes en une troisième.
On introduit pour cela un prédicat ternaire cat(X,Y,Z) qui signifie "X concaténé à Y renvoie Z"
cat(nil, X, X).
cat(cons(X, TL), L, cons(X, TL2)) :- cat(TL, L, TL2)
Les listes chaînées sont tellement utiles que Prolog a une syntaxe standardisée pour les manipuler
[]décrit la liste vide (nil)[Head | Tail]décrit une liste dont on a fixé la tête et la queue (cons(Head,Tail))[X1,X2,X3]décrit une liste à trois éléments (cons(X1,cons(X2,cons(X3,nil))))
Exercice¶
- Définissez un prédicat
pair/1qui est vrai pour les entiers de Peano pairs - Définissez un prédicat
filter_pair/2qui est vrai pour deux listesLetL'siL'est obtenue à partir deLen ne gardant que les entiers de Peano pairs. - Définissez le prédicat
gagne_nim/1(respectivementperd_nim/1) qui est vrai pour un entier de Peano $n$ si le premier joueur d'un jeu de Nim à n allumettes a une stratégie gagnante (respectivement, n'a pas de stratégie gagnante). On rappelle le principe du jeu de Nim: les deux joueurs retirent alternativement 1, 2 ou 3 allumettes, celui qui retire la dernière allumette a perdu.
Solution
pair(zero).
pair(succ(succ(N))) :- pair(N).
filter_pair(nil,nil).
filter_pair(cons(X,Y),cons(X,Z)) :- pair(X), !, filter_pair(Y, Z).
filter_pair(cons(X,Y),Z) :- filter_pair(Y,Z).
ou en syntaxe Prolog
filter_pair([],[]).
filter_pair([X|Y], [X|Z]) :- pair(X), !, filter_pair(Y, Z).
filter_pair([X|Y], Z) :- filter_pair(Y,Z).
gagne(s(X)) :- perd(X).
gagne(s(s(X))) :- perd(X).
gagne(s(s(s(X)))) :- perd(X).
perd(s(zero)).
perd(s(s(s(X)))) :- gagne(X), gagne(s(X)), gagne(s(s(X))).
Unification¶
Une substitution $\sigma$ unifie deux termes $t$ et $t'$ si $t\sigma=t'\sigma$ (au sens de l'égalité entre deux arbres).
Par exemple, cons(s(X),cons(X,nil)) et cons(s(s(Z)),T) a pour unificateur
[X <- s(Z), T<-cons(s(Z),nil)].
On a vu la semaine dernière que l'interprète Prolog repose sur le calcul d'un unificateur le plus général (MGU) de deux atomes. Cette semaine, on va étendre l'algorithme du calcul du MGU à des termes qui peuvent contenir des symboles de fonction, de sorte à pouvoir étendre notre interpréteur Datalog en un interpréteur Prolog (cf TP).
On va commencer par généraliser le problème et considérer un système d'équations $S=$
$$ t_1\sim u_1\quad \wedge \quad t_2\sim u_2\quad \wedge \quad \ldots\quad \wedge \quad t_n\sim u_n $$
et on va chercher une substitution la plus générale $\sigma$ telle que pour tout $i$ $t_i\sigma=u_i\sigma$.
Rappel: on note $\wedge$ le "et" logique
Système résolu¶
Le système d'équation $S$ est résolu s'il est de la forme $$ X_1\sim t_1\quad \wedge \quad X_2\sim t_2\quad \wedge \quad\ldots\quad \wedge \quad X_n\sim t_n $$ et si les $X_i$ qui n'apparaissent qu'une seule fois dans $S$ (autrement dit, pour tout i,j $X_i$ n'apparait pas dans $t_j$).
La solution la plus générale d'un système résolu est la substitution $[X_1\leftarrow t_1,\ldots, X_n\leftarrow t_n]$
Algorithme de Robinson¶
Nous allons voir un algorithme qui ramène un système d'équations quelconque à un système résolu équivalent. Il s'agit d'une reformulation de ce qui est connu sous le nom d'algorithme de Robinson (la présentation suit celle de Comon$^1$, et avant lui Martelli et Montanari).
$^1$ voir page 32
Trivial¶
$ t\sim t\quad\wedge\quad S \qquad \Longrightarrow \qquad S $
Decompose¶
$ f(t_1,\ldots,t_n)\sim f(u_1,\ldots u_n) \qquad \Longrightarrow \qquad t_1\sim u_1\quad \wedge \ldots\wedge\quad t_n\sim u_n $
Symbol Clash¶
$ f(\ldots)\sim g(\ldots) \qquad \Longrightarrow \qquad \bot $
Orient¶
si $t$ n'est pas une variable, $\qquad$ $ t\sim X \qquad \Longrightarrow \qquad X\sim t $
Occurs Check¶
si $X$ apparait dans $t$, $\qquad$ $ X\sim t \qquad \Longrightarrow \qquad \bot $
Variable Elimination¶
si $X$ n'apparait pas dans $t$, $\qquad$ $ X\sim t\quad \wedge\quad S \qquad \Longrightarrow \qquad X\sim t\quad \wedge\quad S[X\leftarrow t] $
Exercice¶
Mettez en forme résolue les systèmes suivants
add(s(s(X)),add(Y,X))$\sim$add(Z,add(Z,Z)f(X,g(X),c)$\sim$f(c,Y,Y)add(zero,s(X))$\sim$add(Y,s(zero))$\quad\wedge\quad$add(X,s(zero))$\sim$add(Z,s(Z))
add(s(s(X)),add(Y,X))$\sim$add(Z,add(Z,Z)
(Decompose)
$\Rightarrow$ s(s(X)) $\sim$ Z $\quad\wedge\quad$ add(Y,X) $\sim$ add(Z,Z)
(Orient)
$\Rightarrow$ Z $\sim$ s(s(X)) $\quad\wedge\quad$ add(Y,X) $\sim$ add(Z,Z)
(Decompose)
$\Rightarrow$ Z $\sim$ s(s(X)) $\quad\wedge\quad$ Y $\sim$ Z $\quad\wedge\quad$ X $\sim$ Z
(Variable Elimination)
$\Rightarrow$ Z $\sim$ s(s(X)) $\quad\wedge\quad$ Y $\sim$ s(s(X)) $\quad\wedge\quad$ X $\sim$ s(s(X))
(Occurs Check)
$\Rightarrow$ $\bot$
f(X,g(X),c)$\sim$f(c,Y,Y)
(Decompose)
$\Rightarrow$ X $\sim$ c $\quad\wedge\quad$ g(X) $\sim$ Y $\quad\wedge\quad$ c $\sim$ Y
(Orient)
$\Rightarrow$ X $\sim$ c $\quad\wedge\quad$ Y $\sim$ g(X) $\quad\wedge\quad$ c $\sim$ Y
(Variable Elimination)
$\Rightarrow$ X $\sim$ c $\quad\wedge\quad$ Y $\sim$ g(X) $\quad\wedge\quad$ c $\sim$ g(X)
(Symbol Clash)
$\Rightarrow$ $\bot$
add(zero,s(X))$\sim$add(Y,s(zero))$\quad\wedge\quad$add(X,s(zero))$\sim$add(Z,s(Z))
(Decompose)
$\Rightarrow$ zero $\sim$ Y $\quad\wedge\quad$ s(X) $\sim$ s(zero) $\quad\wedge\quad$ add(X,s(zero)) $\sim$ add(Z,s(Z))
(Decompose)
$\Rightarrow$ zero $\sim$ Y $\quad\wedge\quad$ s(X) $\sim$ s(zero) $\quad\wedge\quad$ X $\sim$ Z $\quad\wedge\quad$ s(zero) $\sim$ s(Z)
(Decompose)
$\Rightarrow$ zero $\sim$ Y $\quad\wedge\quad$ X $\sim$ zero $\quad\wedge\quad$ X $\sim$ Z $\quad\wedge\quad$ s(zero) $\sim$ s(Z)
(Decompose)
$\Rightarrow$ zero $\sim$ Y $\quad\wedge\quad$ X $\sim$ zero $\quad\wedge\quad$ X $\sim$ Z $\quad\wedge\quad$ zero $\sim$ Z
...
...
$\Rightarrow$ zero $\sim$ Y $\quad\wedge\quad$ X $\sim$ zero $\quad\wedge\quad$ X $\sim$ Z $\quad\wedge\quad$ zero $\sim$ Z
(Orient)
$\Rightarrow$ Y $\sim$ zero $\quad\wedge\quad$ X $\sim$ zero $\quad\wedge\quad$ X $\sim$ Z $\quad\wedge\quad$ zero $\sim$ Z
(Variable Elimination)
$\Rightarrow$ Y $\sim$ zero $\quad\wedge\quad$ X $\sim$ zero $\quad\wedge\quad$ zero $\sim$ Z $\quad\wedge\quad$ zero $\sim$ Z
(Orient)
$\Rightarrow$ Y $\sim$ zero $\quad\wedge\quad$ X $\sim$ zero $\quad\wedge\quad$ Z $\sim$ zero $\quad\wedge\quad$ zero $\sim$ Z
(Variable Elimination)
$\Rightarrow$ Y $\sim$ zero $\quad\wedge\quad$ X $\sim$ zero $\quad\wedge\quad$ Z $\sim$ zero $\quad\wedge\quad$ zero $\sim$ zero
(Trivial)
$\Rightarrow$ Y $\sim$ zero $\quad\wedge\quad$ X $\sim$ zero $\quad\wedge\quad$ Z $\sim$ zero
Application: algorithme de Hindley - Milner¶
Dans certains langages fonctionnels (OCaml et Haskell, un peu Rust, un peu Java...) le compilateur est capable d'inférer les types du programme sans que l'utilisateur ait à les écrire.
Nous allons maintenant étudier un algorithme d'inférence de type dû à Curry et Feys (mais qu'on appele algorithme de Hindley-Milner, ou juste Hindley...).
Nous allons voir cet algorithme sur un tout petit langage fonctionnel qui correspond au lambda-calcul, mais dont le principe se généralise aisément à des langages plus complexes, ce qui permettra d'avoir une idée (très simplifiée) de la façon dont les compilateurs procèdent pour inférer les types.
Lambda-expressions¶
Une lambda-expression $e$ est soit une variable $x$, soit un fonction anonyme $\lambda x.e$, soit l'application de deux lambda-expressions $e_1\ e_2$. En OCaml cela correspond à ce que l'on peut écrire en utilisant le mot-clé fun, ->, les parenthèses, l'espace (application de fonction), et les variables.
Exemples de lambda-expressions et leur écriture en syntaxe Caml:
- $\lambda x.\,x\ y$ s'écrit en Caml
fun x -> (x y)(les parenthèses sont inutiles) - $\lambda x.\,\lambda y.\, x\ y$ s'écrit en Caml
fun x -> (fun y -> x y)(les parenthèses sont inutiles) - $(\lambda x.\,x)\ (\lambda y.\, y)$ s'écrit
(fun x -> x) (fun y -> y): les parenthèses sont nécessaires
Si toutes les variables sont sous le scope du $\lambda$/fun qui les introduit, on dit que la lambda-expression est close.
- $\lambda x.\, x\ y$ n'est pas clos ($y$ n'est pas introduit par un $\lambda$)
- $(\lambda x.\, x)\ (\lambda y.\, y)$ est clos
- $(\lambda x.\, x)\ (\lambda y.\ x)$ n'est pas clos
Types simples¶
Un type $\tau$ est soit une variable de type $\alpha,\beta,\ldots$('a,, 'b, etc), soit le type $\tau_1\to\tau_2$ des fonctions qui prennent un argument de type $\tau_1$ et renvoient une valeur de type $\tau_2$. On note $\vdash e:\tau$ si la lambda-expression close $e$ a le type $\tau$.
On peut aussi utiliser la syntaxe Caml pour écrire des types simples.
Exemples:
- $\vdash \lambda x.\,x : \alpha\to\alpha$ . C'est la fonction identité,
fun x -> x: 'a -> 'aen OCaml - $\vdash \lambda x.\,\lambda y.\, x : \alpha\to\beta\to\alpha$. C'est la fonction "première projection",
fun x -> fun y -> x: 'a -> 'b -> 'aen OCaml - $\vdash \lambda x.\,\lambda y.\ x\, y : (\alpha\to\beta)\to\alpha\to\beta$. C'est la fonction "appliquer" (
(@@)en OCaml) qui prend une fonction x et un argument y et qui renvoie le résultat de la fonction x sur l'argument y.
Rappel: par convention $\to$ est associative à droite, donc le type ci-dessus doit être compris comme $(\alpha \to \beta)\to(\alpha\to\beta)$.
Principe de l'algorithme¶
- On renomme les variables de sorte que deux variables liées par des $\lambda$ différents ont des noms différents; par exemple, on renomme $(\lambda x.\, x)\ (\lambda x.\, x)$ en $(\lambda x.\, x)\ (\lambda y.\, y)$. Cette étape n'est pas essentielle mais simplifie la présentation.
- On introduit une inconnue de type pour chaque sous-expression.
- Chaque sous-expression non réduite à une variable (donc de la forme $\lambda x.\ e$ ou $e_1\ e_2$) génère une équation de types à résoudre.
- On représente les types par des termes et on résoud le système d'équation avec l'algorithme d'unification.
- Le type inféré pour l'expression considéré est la solution pour la variable de type associée
Exemple: on veut inférer le type de $\lambda x.\, \lambda y.\, x\ (y\ x)$.
- pas besoin de renommer dans ce cas-là
- on introduit les inconnues de type $\alpha_1,\alpha_2,\alpha_3,\alpha_4,\alpha_5,\alpha_6$ associées aux sous-expressions comme suit
- $x: \alpha_1$, $y:\alpha_2$
- $y\ x: \alpha_3$
- $x\ (y\ x): \alpha_4$
- $\lambda y.\, x\ (y\ x) : \alpha_5$
- $\lambda x.\, \lambda y. x\ (y\ x) : \alpha_6$
- on collecte les équations de typage
$y\ x: \alpha_3$ signifie que $y$ (de type $\alpha_2$) est une fonction qui renvoie du $\alpha_3$ (le type de $y\ x$) et qui prend des arguments de type $\alpha_1$ (le type de $x$). On a donc l'équation $$ \alpha_2 \quad \sim\quad \alpha_1\to\alpha_3 $$
$\lambda y.\, x\ (y\ x): \alpha_5$ signifie que $\alpha_5$ est le type des fonctions qui prennent un argument de type $\alpha_2$ et renvoient une valeur de type $\alpha_4$ $$ \alpha_5 \quad \sim\quad \alpha_2\to\alpha_4 $$
on procède de même pour $x\ (y\ x)$ et $\lambda x.\, \lambda y. x\ (y\ x)$
- on aboutit au système d'équations
$$ \alpha_2 \quad \sim\quad \alpha_1\to\alpha_3 \qquad\wedge\qquad \alpha_1 \quad \sim\quad \alpha_3\to\alpha_4 \qquad\wedge\qquad \alpha_5\quad\sim\quad \alpha_2\to \alpha_4 \qquad\wedge\qquad \alpha_6\quad\sim\quad \alpha_1\to \alpha_5 $$ Que l'on réécrit en forme résolue
$ \alpha_2 \quad \sim\quad \alpha_1\to\alpha_3 \qquad\wedge\qquad \alpha_1 \quad \sim\quad \alpha_3\to\alpha_4 \qquad\wedge\qquad \alpha_5\quad\sim\quad \alpha_2\to \alpha_4 \qquad\wedge\qquad \alpha_6\quad\sim\quad \alpha_1\to \alpha_5 $
(Variable Elimination, $\alpha_2$) $\Rightarrow$
$ \alpha_2 \quad \sim\quad \alpha_1\to\alpha_3 \qquad\wedge\qquad \alpha_1 \quad \sim\quad \alpha_3\to\alpha_4 \qquad\wedge\qquad \alpha_5\quad\sim\quad (\alpha_1\to\alpha_3)\to \alpha_4 \qquad\wedge\qquad \alpha_6\quad\sim\quad \alpha_1\to \alpha_5 $
(Variable Elimination, $\alpha_1$) $\Rightarrow$
$ \alpha_2 \quad \sim\quad (\alpha_3\to\alpha_4)\to\alpha_3 \qquad\wedge\qquad \alpha_1 \quad \sim\quad \alpha_3\to\alpha_4 \qquad\wedge\qquad \alpha_5\quad\sim\quad ((\alpha_3\to\alpha_4)\to\alpha_3)\to \alpha_4 \qquad\wedge\qquad \alpha_6\quad\sim\quad (\alpha_3\to\alpha_4)\to \alpha_5 $
(Variable Elimination, $\alpha_5$) $\Rightarrow$
$ \alpha_2 \quad \sim\quad (\alpha_3\to\alpha_4)\to\alpha_3 \qquad\wedge\qquad \alpha_1 \quad \sim\quad \alpha_3\to\alpha_4 \qquad\wedge\qquad \alpha_5\quad\sim\quad ((\alpha_3\to\alpha_4)\to\alpha_3)\to \alpha_4 \qquad\wedge\qquad \alpha_6\quad\sim\quad (\alpha_3\to\alpha_4)\to ((\alpha_3\to\alpha_4)\to\alpha_3)\to \alpha_4 $
La lambda-expression $\lambda x.\,\lambda y.\,x\ (y\ x)$ a donc le type $(\alpha_3\to\alpha_4)\to ((\alpha_3\to\alpha_4)\to\alpha_3)\to \alpha_4$ (la solution trouvée pour $\alpha_6$ dans la forme résolue)
On vérifie aisément qu'on trouve la même chose que Caml
utop # fun x -> fun y -> x (y x);;
- : ('a -> 'b) -> (('a -> 'b) -> 'a) -> 'b = <fun>
Exercice¶
Appliquez l'algorithme de Hindley-Milner pour inférer le type des lambda-expressions suivantes, lorsqu'elles sont typables avec un type simple
- $\lambda x.\, (x\ (\lambda y.\, y))$
- $\lambda x.\, \lambda y.\, \lambda z.\, x\ z\ (y\ z)$
- $\lambda x.\, (x\ (\lambda y.\, x))$
Implémentation Prolog de l'algorithme de Hindley-Milner¶
Pour formaliser l'algorithme précédent on va raisonner par récurrence sur la lambda-expression dont on souhaite inférer le type. Ce faisant, on va devoir raisonner sur des sous-expressions qui ne sont pas closes, et inférer leur type "sous certaines hypothèses" pour les variables libres.
Un environnement de typage $\Gamma$ est une liste de couples $(x_i,\tau_i)$ variables/type.
On note $\Gamma\vdash e:\tau$ le fait que "sous les hypothèses $\Gamma$ de typage des variables libres (non liées par un $\lambda$), la lambda-expression $e$ est de type $\tau$.
Exemples:
- $[x:\alpha\to\beta,\, y:\alpha] \vdash x\ y : \beta$
- $[x:\alpha\to\beta] \vdash \lambda y.\, x\ y : \alpha\to\beta$
On peut définir $\vdash$ par récurrence structurelle sur $e$ de la façon suivante:
Axiome¶
$\Gamma,x:\tau ⊢ x:\tau$
Affaiblissement¶
si $\Gamma\vdash e:\tau$, alors $\Gamma,x:\tau'\vdash e:\tau$
Intro ->¶
si $\Gamma,x:\tau_1 \vdash e:\tau_2$, alors $ \Gamma,\vdash \lambda x.\, e:\tau_1\to\tau_2$
Elim ->¶
si $\Gamma\vdash e_1:\tau\to\tau'$ et $\Gamma\vdash e_2:\tau$, alors $\Gamma\vdash e_1\ e_2:\tau'$
Pour implémenter l'algorithme de Hindley-Milner en Prolog, on va simplement reformuler la définition de $\vdash$ en Prolog.
Il suffira ensuite de faire une requête pour inférer le type d'une expression, Prolog calculera tout seul le système d'équations de type et le résoudra.
Nous allons utiliser les symboles de fonctions et les prédicats suivants:
arrow/2pour représenter la flèche entre deux typeslambda/2pour représenter une fonction anonymeapp/2pour représenter une application- les identifiants prolog (
x,y,...) pour représenter les variables des lambda-expressions []et[X|Y]pour les listestype/3pour la relation $\vdash$
Exemples:
- la lambda-expression $\lambda x.\, x\ x$ est représentée par le terme
lambda(x,app(x,x)) - le type $(\alpha\to\beta)\to\gamma$ est représenté par le terme
arrow(arrow(Alpha,Beta),Gamma) - l'environnement de typage $[x:\alpha,y:\alpha\to\beta]$ est représenté par la liste Prolog
[x,Alpha,y,arrow(Alpha,Beta)] - la relation $\Gamma,x:\alpha\vdash y:\beta$ est représentée par l'atome
type([X,Alpha| Gamma],y,Beta)
Cela nous conduit au code Prolog suivant
% Axiome
type([X, Alpha | _], X, Alpha).
% Affaiblissement
type([X, Alpha | Gamma], E, Tau) :- type(Gamma, E, Tau).
% Intro ->
type(Gamma, lambda(X,E), arrow(Tau1,Tau2)) :-
type([X, Tau1 | Gamma], E, Tau2).
% Elim ->
type(Gamma, app(E1, E2), Tau) :-
type(Gamma, E1, arrow(Tau2, Tau)),
type(Gamma, E2, Tau2).
Je peux ensuite écrire une requête qui vérifie le type d'une expression, ou qui l'infère.
Exemples:
- $\lambda x.\,\lambda y.\, x\ y$ est bien de type $(\alpha\to\beta)\to\alpha\to\beta$?
?- type([], lambda(x,lambda(y,app(x,y))), arrow(arrow(Alpha,Beta),arrow(Alpha,Beta))).- renvoie
true
- quel est le type le plus général de $\lambda x.\,\lambda y.\, x\ y$?
?- type([], lambda(x,lambda(y,app(x,y))), Tau).- renvoie
[Tau <- arrow(arrow(Alpha,Beta),arrow(Alpha,Beta)))].
Limitations¶
Notre implémentation Prolog de l'algorithme de Hindley n'est pas encore tout à fait au point.
Par exemple, ?- type([], lambda(x,app(x,x))), Tau). renvoie une solution qui est [Tau<-arrow(Tau,Tau2)]. Pourtant ce terme n'est pas typable!
Le problème vient du fait que Prolog fait de l'unification sur des termes qui peuvent être potentiellement infinis. Dans l'exemple ci-dessus, il infère le "type" $\Big(\big((\ldots\to\alpha)\to\alpha\big)\to\alpha\Big)\to\alpha$
Pour faire de l'unification sur des termes infinis, c'est plus simple que sur des termes finis: on applique les même règles vues précédemment, sauf qu'on n'a plus à se préoccuper de la règle Occurs check.
Autre limitation: on a supposé que les variables introduites par des $\lambda$ étaient toujours différentes. C'est essentiel, sinon on peut se retrouver avec deux fois la même variable dans l'environnement de typage $\Gamma$, à chaque fois avec des types différents.
Exemple: supposons que l'on cherche à typer $\lambda x.\, \lambda x.\, x\ x$. L'algorithme est censé répondre que cette expression n'est pas typable, puisqu'elle est équivalente à $\lambda y.\, \lambda x.\, x\ x$.
Cependant, il arrive à le typer par le raisonnement suivant $$ \begin{array}{ll} & \vdash \lambda x.\, \lambda x.\, x\ x :\alpha\to(\alpha\to\beta)\to\beta \\ \Rightarrow & [x: \alpha] \vdash \lambda x.\, x\ x :(\alpha\to\beta)\to\beta \\ \Rightarrow & [x: \alpha\to\beta, x: \alpha] \vdash x\ x :\beta \\ \Rightarrow & [x: \alpha\to\beta, x: \alpha] \vdash x :\alpha\to\beta \qquad \mbox{et}\qquad [x: \alpha\to\beta, x: \alpha] \vdash x :\alpha\\ \end{array} $$
Et chaque branche réussit en prennant le type qui va bien pour x. En fait, l'hypothèse $x: \alpha\to\beta$ devrait "masquer" l'hypothèse $x: \alpha$ et la branche $[x: \alpha\to\beta, x: \alpha] \vdash x :\alpha$ devrait échouer...
On peut adapter un tout petit peu le programme Prolog pour qu'il devienne correct avec des lambda-expressions qui introduisent plusieurs fois la même variable... la clé est de n'appliquer la règle d'affaiblissement que si la règle d'axiome a échoué! La suite en TP.
Pour aller plus loin...¶
L'algorithme de Damas-Milner est une variante de l'algorithme de Hindley qui permet d'inférer des types polymorphes, avec des variables de type "quantifiée universellement". C'est sur cet algorithme, plus compliqué que celui de l'algorithme de Hindley, que se basent les compilateurs de Caml et Haskell.
L'algorithme de Knuth-Bendix utilise l'unification de termes pour faire de la démonstration automatique, par exemple pour démontrer automatiquement des énoncés comme "tout groupe d'ordre 2 est commutatif".
D'autres algorithmes d'unification en temps polynomial, quasi linéaire, et linéaire (celui vu dans ce cours est en temps exponentiel dans le pire cas)