



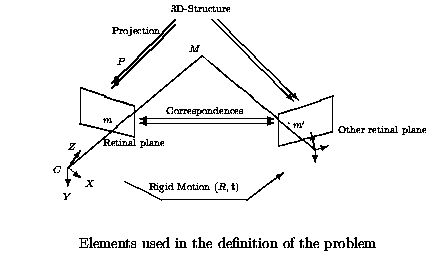
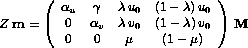
In this model, we distinguish two kinds of parameters:
 and
and 

 |  |
|
| Pure perspective projection | 1 | 1 |
| Weak perspective projection (i.e. affine or orthographic) | 0 | 0 |
| Para-perspective projection | 1 | 0 |
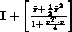 where r=[r0 r1 r2]T
where r=[r0 r1 r2]Tand a translation vector t = [t0 t1 t2]T
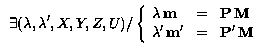
which can be also written as:
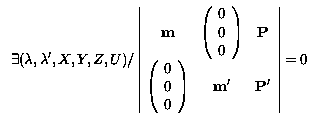
and interpreted as a bilinear form in m and m', so that we can express this result in a more familiar form, using a generalization of the fundamental matrix:

This is easily generalizable to N views.
 which allows to represent the fact that the retina might not be orthogonal with respect to the optical axis and can be approximated to zero or considered as a fixed parameter
which allows to represent the fact that the retina might not be orthogonal with respect to the optical axis and can be approximated to zero or considered as a fixed parameter
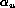 and
and 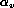 the focal lengths:
the focal lengths:
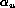 and
and 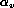 are fixed
are fixed
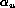 and
and 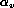 are fixed and known
are fixed and known
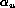 by
by 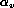 is fixed and precalibrated
is fixed and precalibrated
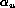 and
and 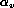 approximed to their 1st order
approximed to their 1st order
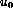 and
and 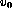 the coordinates of the principal point c:
the coordinates of the principal point c:
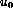 and
and 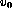 fixed but unknowns
fixed but unknowns
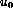 and
and 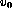 fixed but knowns (for example, fixed at the center of the image)
fixed but knowns (for example, fixed at the center of the image)
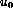 and
and 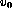 approximed to their 1st order
approximed to their 1st order
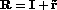

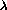 / r =
/ r = 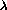 t
t
 t
t 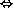 r.t = 0
r.t = 0
 t
t
 r
r
 (t
(t  r)
r) (t2 = 0)
(t2 = 0)  (t
(t  r)
r)
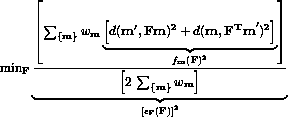
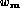 is a weight corresponding to the precision of the match, in fact the inverse of the variance of the precision of the match. The quantity
is a weight corresponding to the precision of the match, in fact the inverse of the variance of the precision of the match. The quantity 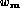 is given in pixels-2, while
is given in pixels-2, while  , the average distance to the epipolar, is in pixel.
, the average distance to the epipolar, is in pixel.

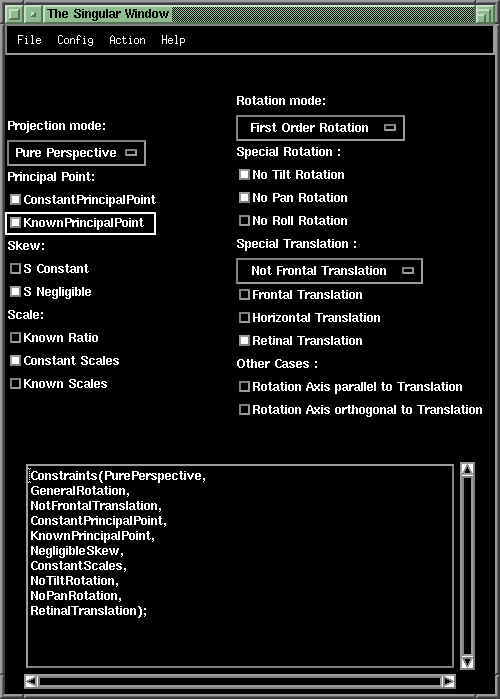





| particular case | residual error |
no rotation, fixed zoom,  null null |
1.00368 |
| pure translation along x | 0.00485771 |
| pure translation along z | 1.00368 |
rotation along x, translation along z, null null |
987.827 |
| zoom and pure translation | 0.955463 |
These results show us that:





| particular case | residual error |
no rotation, fixed zoom,  null null |
1068.44 |
| pure translation along x | 1068.44 |
| pure translation along z | 1068.44 |
rotation along x, translation along z,  null null |
7378.61 |
| pure zoom | 773.026 |
The conclusions are similar to those of the previous experiment. However, we note that the size of residual errors are not normalized with respect to the number of points, ...



French and postscript version of this paper.
