Les équations du problème
Modèle de caméra et repère de référence

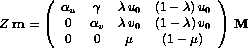
Dans ce modèle, on distingue deux types de paramètres:
- Paramètres modaux:
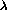 et
et 
- Paramètres intrinsèques: u0, v0 et

Les paramètres modaux déterminent le modèle de projection:
| 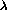 |  |
| Projection perspective pure | 1 | 1 |
| Projection faiblement perspective (i.e. affine ou orthographique) | 0 | 0 |
| Projection para-perspective | 1 | 0 |
Représentation de déplacements rigides
Nous nous intéressons au mouvement d'objets rigides dans la scène et au mouvement propre de la caméra.
Cela signifie que les éléments de la scène vont effectuer un mouvement rigide paramétrisé par une matrice de rotation R s'exprimant sous la forme:
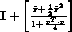 où r=[r0 r1 r2]T
où r=[r0 r1 r2]T
et une translation de vecteur t = [t0 t1 t2]T
Equations du cas général
Considérant deux images consécutives~:
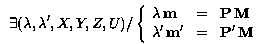
Ce qui peut également s'écrire~:
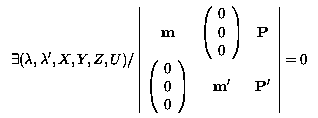
On peut remarquer qu'il s'agit d'une forme bilinéaire en ${\bf m}$ et ${\bf m'}$, ce qui montre que ce résultat peut se mettre sous une forme plus habituelle, utilisant une généralisation de la matrice fundamentale~:

Les cas particuliers
Nous ne traitons dans le cadre de ce papier que les cas particuliers relevant de la modélisation de la caméra et du mouvement de la caméra et de la scène. Les cas relevant des particularités de la scène ne sont pas étudiés dans cet article; on supposera les points dans une position générale (non-coplanaires) ainsi que le mouvement autre qu'une rotation pure, ceci afin d'utiliser exclusivement la matrice F.
Cas particuliers relevant de la modélisation de la caméra
Nous nous intéressons ici aux paramètres modaux et intrinsèques.
Nous avons déjà vu les valeurs possibles pour les paramètre modaux, ce qui se résume à trois cas.
Concernant les paramètres intrinsèques, plusieurs cas sont à considérer:
 mesurant la non-orthogonalité du plan CCD à l'axe optique, peut raisonnablement être négligé dans la plupart des cas ou au pire être considéré constant
mesurant la non-orthogonalité du plan CCD à l'axe optique, peut raisonnablement être négligé dans la plupart des cas ou au pire être considéré constant
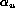 et
et 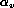 les tailles horizontale et verticale des pixels conduisent à plusieurs cas possibles:
les tailles horizontale et verticale des pixels conduisent à plusieurs cas possibles:
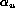 et
et 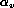 sont constantes
sont constantes
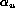 et
et 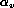 sont constantes et connues
sont constantes et connues
- le rapport de
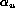 par
par 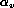 est constant et connu
est constant et connu
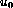 et
et 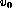 les coordonnées du centre optique peuvent être considérées comme:
les coordonnées du centre optique peuvent être considérées comme:
- constantes mais inconnues
- constantes mais connues (par exemple fixées au centre de l'image)
Cas particuliers relevant du mouvement de la caméra (ou de la scène)
- Mouvement continu - mouvement discret: Dans une séquence d'images, si le mouvement est faible par rapport à la cadence des images, on peut approximer le mouvement à son premier ordre, ce qui concerne uniquement la rotation:
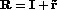
- Autres cas :
- matrice de rotation R: nullité d'une ou de plusieurs composantes du vecteur r
r0 = 0 et/ou r1 = 0 et/ou r2 = 0
- vecteur de translation t: nullité d'une ou deux composantes de t
- (t0 = 0) ou (t1 = 0) ou (t2 = 0)
- ou [(t0 = 0) et (t1 = 0)]
- ou [(t0 = 0) et (t2 = 0)]
- ou [(t1 = 0) et (t2 = 0)]
- parallélisme: r // t
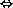

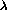 / r =
/ r = 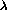 t
t
- orthogonalité: r
 t
t  r.t = 0
r.t = 0
Contraintes: compatibilité - redondance - consistance
L'ensemble des contraintes est formé des contraintes dites atomiques car élémentaires (vues précédemment) et des contraintes dites moléculaires constituées par des ``ET'' logique entre contraintes atomiques exceptées les combinaisons non-possibles.
En effet, si nous combinons les contraintes de non-nullité de la translation, de parallélisme et orthogonalité de la translation et de l'axe de rotation, nous aboutissons à une impossibilité.
D'autre part, si on compare:
(r0 = 0)  (t
(t  r)
et (t1 = 0)
r)
et (t1 = 0)  (t2 = 0)
(t2 = 0)  (t
(t  r)
on s'aperçoit qu'on obtient la même contrainte dans les deux cas, ce qui montre une redondance des contraintes moléculaires, ne permettant pas ainsi de nommer les contraintes moléculaires en fonction des contraintes atomiques les constituant.
r)
on s'aperçoit qu'on obtient la même contrainte dans les deux cas, ce qui montre une redondance des contraintes moléculaires, ne permettant pas ainsi de nommer les contraintes moléculaires en fonction des contraintes atomiques les constituant.
Les cas particuliers sont les contraintes moléculaires vérifiant les propriétés suivantes, et ceci dans un but de correspondre à des cas physiquement réalisables:
- un et un seul modèle de caméra doit être choisi
- un et un seul mode de rotation doit être choisi
- la translation ne doit pas être nulle (on fixe alors au moins une composante à une valeur unitaire)
- la projection du centre de l'image appartient à l'image
D'autre part, les contraintes ne sont pas forcément suffisantes pour résoudre le
problème. Dans ce cas, on peut, soit se limiter aux éléments déterminables, soit
ajouter des contraintes ``par défaut'' afin d'effectuer la résolution complète.
Utilisation des particularités
- déterminer le mode de projection de la caméra
- déterminer les paramètres de calibration (ceux qui sont constants)
- déterminer le type de mouvement et si possible ses caractéristiques (direction de translation, axe de rotation, angle de rotation)
- éventuellement, segmenter les points en ensembles de points rigidement liés





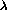 et
et 

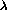

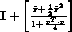 où r=[r0 r1 r2]T
où r=[r0 r1 r2]T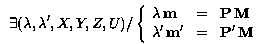
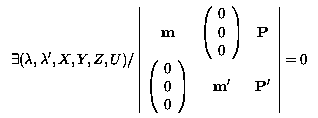

 mesurant la non-orthogonalité du plan CCD à l'axe optique, peut raisonnablement être négligé dans la plupart des cas ou au pire être considéré constant
mesurant la non-orthogonalité du plan CCD à l'axe optique, peut raisonnablement être négligé dans la plupart des cas ou au pire être considéré constant
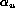 et
et 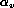 les tailles horizontale et verticale des pixels conduisent à plusieurs cas possibles:
les tailles horizontale et verticale des pixels conduisent à plusieurs cas possibles:
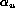 et
et 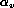 sont constantes
sont constantes
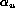 et
et 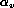 sont constantes et connues
sont constantes et connues
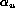 par
par 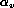 est constant et connu
est constant et connu
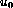 et
et 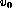 les coordonnées du centre optique peuvent être considérées comme:
les coordonnées du centre optique peuvent être considérées comme:
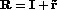
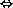

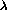 / r =
/ r = 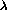 t
t
 t
t 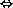 r.t = 0
r.t = 0
 (t
(t  r)
r) (t2 = 0)
(t2 = 0)  (t
(t  r)
r)
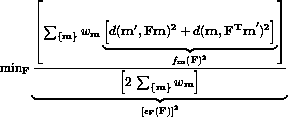
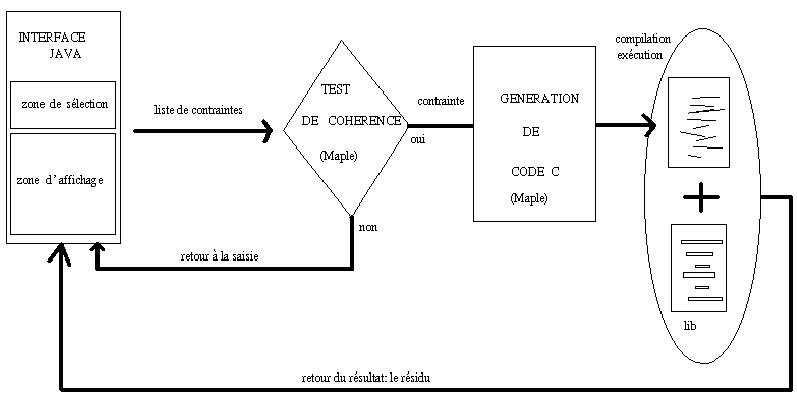
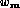 est un poids correspondant à la précision de l'appariement, en réalité, l'inverse de la variance de la précision de l'appariement. La quantité
est un poids correspondant à la précision de l'appariement, en réalité, l'inverse de la variance de la précision de l'appariement. La quantité  est donnée en inverse de pixels au carré, tandis que
est donnée en inverse de pixels au carré, tandis que  , la distance moyenne à l'épipole, est en pixels.
, la distance moyenne à l'épipole, est en pixels.






 nul
nul nul
nul




 nul
nul nul
nul


